初中数学相似多边形的性质试题

如图，在直角梯形ABCD中，AB∥DC，∠D = 90^o，AC⊥BC，
AB =" 10cm" , BC = 6cm，F点以2 cm／秒的速度在线段AB上由A向B匀速运动， E点同时以1 cm／秒的速度在线段BC上由B向C匀速运动，设运动时间为 t 秒 ( 0 < t < 5 )．

（1）求证：△ A C D ∽△ B A C ；
（2）求DC的长；
（3）设四边形AFEC的面积为 y ，求 y关于t的函数关系式．

将三角形纸片（△ABC）按如图所示的方式折叠，使点B落在边AC上，记为点B′，折痕为EF．已知AB＝AC＝3，BC＝4，若以点B′，F，C为顶点的三角形与△ABC相似，那么BF的长度是          ．

如图，两处被池塘隔开，为了测量两处的距离，在外选一适当的点，连接，并分别取线段的中点，测得=20m，则=__________m．

如图，△ABC中，A，B两个顶点在x轴的上方，点C的坐标是(-1，0)．以点C为位似中心，在x轴的下方作△ABC的位似图形，并把△ABC的边长放大到原来的2倍，记所得的像是△A′B′C．
设点B的对应点B′的横坐标是a，则点B的横坐标是

A．	B．
C．	D．

（本小题满分6分）
如图，D，E分别是的AB，AC边上的点，∽．
已知AD：DB=1：2，BC=18 cm，求DE的长．

已知线段cm，cm，则线段，的比例中项为         cm.

线段4和1的比例中项为是         。

如图1，在平面直角坐标系中有一个，点，点，将其沿直线AC翻折，翻折后图形为.动点P从点O出发，沿折线的方向以每秒2个单位的速度向B运动，同时动点Q从点B出发，在线段BO上以每秒1个单位的速度向点O运动，当其中一个点到达终点时，另一点也随之停止运动.设运动的时间为t(秒).
设的面积为S，求S与t之间的函数关系式，并写出自变量t的取值范围；
如图2，固定，将绕点C逆时针旋转，旋转后得到的三角形为，设与AC交于点D，当时，求线段CD的长；
如图3，在绕点C逆时针旋转的过程中，若设所在直线与OA所在直线的交点为E，是否存在点E使为等腰三角形，若存在，求出点E的坐标，若不存在，请说明理由.

与相似且面积的比为，则与的周长比为          .

如图.AD、AH分别是△ABC（其中AB＞AC）的角平分线、高线，M点是AD的中点，△MDH的外接圆交CM于E，求证∠AEB=90°。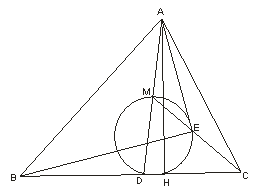

如图，已知△ABC的面积是的等边三角形，△ABC∽△ADE，AB=2AD，∠BAD=45°，AC与DE相交于点F，则△AEF的面积等于__________（结果保留根号）.

已知a=4,c=9，若b是a,c的比例中项,则b等于            .

如图，在△ABC中，AB=8，BC=7，AC=6，延长边BC到点P，使得△PAB与△PCA相似.则PC的长是(    ).

A．7

B．8

C．9

D．10

(25分)如图，在Rt△ABC中，∠B=90°，它的内切圆分别与边BC、CA、AB相切于点D、E、F，联结AD与内切圆相交于另一点P，联结PC、PE、PF.已知PC⊥PF.求证:
(1)EP/DE=PD/DC;(2)△EPD是等腰三角形.

如图，△ABC中，，．点P在△ABC内，且，求△ABC的面积．