初中数学相似多边形的性质试题

已知Rt△ABC中，AC=3，BC= 4，过直角顶点C作CA₁⊥AB，垂足为A₁，再过A₁作A₁C₁⊥BC， 垂足为C₁，过C₁作C₁A₂⊥AB，垂足为A₂，再过A₂作A₂C₂⊥BC，垂足为C₂，…，这样一直做下去，得到了一组线段CA₁，A₁C₁，C₁A₂，…，则CA₁=      ，       .

如图，在△ABC中，DE∥BC，DF∥AC，则下列比例式一定成立的是（   ）

A．

B．

C．

D．

如图，平行四边形ABCD，DE交BC于F，交AB的延长线于E，且∠EDB=∠C.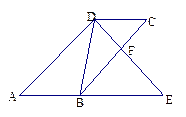

（1）求证：△ADE∽△DBE；
（2）若DE=9cm，AE=12cm，求DC的长。

如图，△ABC中，AB=8厘米，AC=16厘米，点P从A出发，以每秒2厘米的速度向B运动，点Q从C同时出发，以每秒3厘米的速度向A运动，其中一个动点到端点时，另一个动点也相应停止运动，那么，当以A、P、Q为顶点的三角形与△ABC相似时，运动时间为_________________

 

如图，O是△ABC的重心，AN，CM相交于点O，那么△MON与△AOC的面积的比是_______________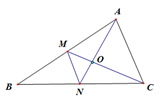

在比例尺1:50000的地图上，量得A、B两地的距离为4cm，则A、B两地的实际距离是___________千米

(本题满分10分)如图，已知一矩形ABCD，若把△ABE沿折痕BE向上翻折，A点恰好落在DC上，设此点为F，且这时AE:ED=5:3，BE=5，这个矩形的长宽各是多少？

如图，在梯形ABCD中，AD∥BC，∠B=90°，∠C=45°，AD=1，BC=4，E为AB中点，EF∥DC交BC于点F，求EF的长．

如图，已知EF//BC，且AE∶BE=1∶2，若△AEF的面积为4，
则△ABC的面积为________________.

(满分l4分)如图，点P是双曲线y=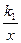(k₁<0，x<0)上一动点，过点P作x轴，y轴的垂线，分别交x轴，y轴于A，B两点，交双曲线y= 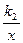(0<k₂<︱k₁︱)于E，F两点．
(1)图①中，四边形PEOF 的面积S₁=__________(用含k₁，k₂的式子表示)；
(2)图②中，设点P坐标为(-4，3)．
①判断EF与AB的位置关系，并证明你的结论；
②记S₂=S_△PEF-S_△OEF，S₂是否有最小值?若有，求出其最小值；若没有，请说明理由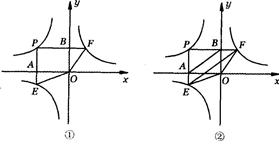

(满分l4分)已知：抛物线y=x²-(a+2)x+9的顶点在坐标轴上．
(1)求a的值；
(2)若该抛物线的顶点C在x轴的正半轴上，而此抛物线与直线Y=x+9交于A，B两点，且A点在B点左侧，P为线段AB上的点(A，B两端点除外)．过点P作x轴的垂线与抛物线交于点Q(可在图中画示意图)．问：

①线段AB上是否存在这样的点P，使得PQ的长等于6?若存在，请求出点P的坐标；若不存在，请说明理由．
②线段AB上是否存在这样的点P，使得△ABQ∽△OAC?若存在，请求出此时点Q的坐标；若不存在，请说明理由．

(满分l4分)如图，已知AB为⊙O的直径，弦CD⊥AB，垂足为点H．
(1)求证：AH·AB=AC²；
(2)若过点A的直线与弦CD(不含端点)相交于点E，与⊙O相交于点F，求证：AE·AF=AC²；
(3)若过点A的直线与直线CD相交于点P，与⊙O相交于点Q，判断AP·AQ=AC²是否成立(不必证明)．

在△ABC中，若D，E分别是边AB，AC上的点，且DE∥BC，AD=1，DB=2，则△ADE与△ABC的面积比为__________．

如图，若A，B，C，P，Q，甲，乙，丙，丁都是方格纸中的格点，为使△ABC∽△PQR，则点R应是甲，乙，丙，丁四点中的

A．甲

B．乙

C．丙

D．丁

(满分l4分)如图已知直线l₁:y=x+与直线l₂:y=2x+16相交于点C，l₁，l₂分别交x轴于A，B两点．矩形DEFG的顶点D，E分别在直线l₁，l₂上，顶点F，G都在X轴上，且点G与点B重合．
(1)求△ABC的面积；
(2)求矩形DEFG的边DE与EF的长；
(3)若此时矩形DEFG，沿x轴的反方向以每秒l个单位长度的速度平移，设移动时间为t 5(0≤t≤12)，矩形DEFG与△ABC重叠部分的面积为S，求S关于t的函数关系式，并写出相应的t的取值范围．