如图,在 中, ,以 的边 为直径作 ,交 于点 ,过点 作 ,垂足为点 .
(1)试证明 是 的切线;
(2)若 的半径为5, ,求此时 的长.

如图1,四边形 的对角线 , 相交于点 , , .
(1)过点 作 交 于点 ,求证: ;
(2)如图2,将 沿 翻折得到 .
①求证: ;
②若 ,求证: .

问题探究:
小红遇到这样一个问题:如图1, 中, , , 是中线,求 的取值范围.她的做法是:延长 到 ,使 ,连接 ,证明 ,经过推理和计算使问题得到解决.
请回答:(1)小红证明 的判定定理是: ;
(2) 的取值范围是 ;
方法运用:
(3)如图2, 是 的中线,在 上取一点 ,连结 并延长交 于点 ,使 ,求证: .
(4)如图3,在矩形 中, ,在 上取一点 ,以 为斜边作 ,且 ,点 是 的中点,连接 , ,求证: .

如图,点 在以 为直径的 上,点 是半圆 的中点,连接 , , , .过点 作 交 的延长线于点 .
(1)求证:直线 是 的切线;
(2)若 , ,求 , 的长.
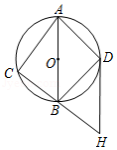
如图,在 中, ,将 沿直线 翻折得到 ,连接 交 于点 . 是线段 上的点,连接 . 是 的外接圆与 的另一个交点,连接 , .
(1)求证: 是直角三角形;
(2)求证: ;
(3)当 , 时,在线段 上存在点 ,使得 和 互相平分,求 的值.

如图, 内接于 , 为 的直径, , ,连结 ,弦 分别交 , 于点 , ,其中点 是 的中点.
(1)求证: .
(2)求 的长.

【基础巩固】
(1)如图1,在 中, 为 上一点, .求证: .
【尝试应用】
(2)如图2,在 中, 为 上一点, 为 延长线上一点, .若 , ,求 的长.
【拓展提高】
(3)如图3,在菱形 中, 是 上一点, 是 内一点, , , , , ,求菱形 的边长.

如图,在 中, , , .
(1)求 边上的高线长.
(2)点 为线段 的中点,点 在边 上,连结 ,沿 将 折叠得到 .
①如图2,当点 落在 上时,求 的度数.
②如图3,连结 ,当 时,求 的长.

已知在 中, , 是 边上的一点,将 沿着过点 的直线折叠,使点 落在 边的点 处(不与点 , 重合),折痕交 边于点 .
(1)特例感知 如图1,若 , 是 的中点,求证: ;
(2)变式求异 如图2,若 , , ,过点 作 于点 ,求 和 的长;
(3)化归探究 如图3,若 , ,且当 时,存在两次不同的折叠,使点 落在 边上两个不同的位置,请直接写出 的取值范围.

如图,在正方形 中,点 在 边上,连接 , 的平分线 与 边交于点 ,与 的延长线交于点 .设 .
(1)若 , ,求线段 的长.
(2)连接 ,若 ,
①求证:点 为 边的中点.
②求 的值.

如图,在 中,点 , , 分别在 , , 边上, , .
(1)求证: .
(2)设 ,
①若 ,求线段 的长;
②若 的面积是20,求 的面积.

如图, 为线段 外一点.
(1)求作四边形 ,使得 ,且 ;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的四边形 中, , 相交于点 , , 的中点分别为 , ,求证: , , 三点在同一条直线上.

四边形 是边长为2的正方形, 是 的中点,连结 ,点 是射线 上一动点(不与点 重合),连结 ,交 于点 .
(1)如图1,当点 是 边的中点时,求证: ;
(2)如图2,当点 与点 重合时,求 的长;
(3)在点 运动的过程中,当线段 为何值时, ?请说明理由.

如图,四边形 是菱形,点 为对角线 的中点,点 在 的延长线上, ,垂足为 ,点 在 的延长线上, ,垂足为 ,
(1)若 ,求证:四边形 是菱形;
(2)若 , 的面积为16,求菱形 的面积.
试题篮
()