初中数学相似三角形的判定与性质试题

如图1和图2，在中，，，．点在边上，点，分别在，上，且．点从点出发沿折线匀速移动，到达点时停止；而点在边上随移动，且始终保持．

（1）当点在上时，求点与点的最短距离；

（2）若点在上，且将的面积分成上下两部分时，求的长；

（3）设点移动的路程为，当及时，分别求点到直线的距离（用含的式子表示）；

（4）在点处设计并安装一扫描器，按定角扫描区域（含边界），扫描器随点从到再到共用时36秒．若，请直接写出点被扫描到的总时长．

若 $\mathit{\Delta ABC}$ 的每条边长增加各自的 $10\%$ 得△ $A\text{'}B\text{'}C\text{'}$ ，则 $\angle B\text{'}$ 的度数与其对应角 $\angle B$ 的度数相比 $($ 　　 $)$

A．	增加了 $10\%$	B．	减少了 $10\%$
C．	增加了 $(1+10\%)$	D．	没有改变

如图，中，，，为内部一点，且．

（1）求证：；

（2）求证：；

（3）若点到三角形的边，，的距离分别为，，，求证．

如图，在 $\text{Rt}\Delta \text{ABC}$ 中， $\angle \mathit{ACB}=90°$ ， $\mathit{AC}=6$ ， $\mathit{BC}=12$ ，点 $D$ 在边 $\mathit{BC}$ 上，点 $E$ 在线段 $\mathit{AD}$ 上， $\mathit{EF}\perp \mathit{AC}$ 于点 $F$ ， $\mathit{EG}\perp \mathit{EF}$ 交 $\mathit{AB}$ 于点 $G$ ．若 $\mathit{EF}=\mathit{EG}$ ，则 $\mathit{CD}$ 的长为 $($ 　　 $)$

A．

3.6

B．

4

C．

4.8

D．

5

如图，在矩形中，是边的中点，连接交对角线于点，若，，则的长为　　．

如图，在中，、分别为，的中点．若，则　　．

已知正方形，点为边的中点．

（1）如图1，点为线段上的一点，且，延长、分别与边、交于点、．

①求证：；

②求证：．

（2）如图2，在边上取一点，满足，连接交于点，连接并延长交于点，求的值．

如图1，，分别在射线，上，且为钝角，现以线段，为斜边向的外侧作等腰直角三角形，分别是，，点，，分别是，，的中点．

（1）求证：；

（2）延长，交于点．

①如图2，若，求证：为等边三角形；

②如图3，若，求大小和的值．

如图，在矩形纸片中，，，点在上，将沿折叠，点恰落在边上的点处；点在上，将沿折叠，点恰落在线段上的点处，有下列结论：

①；②；③；④．

其中正确的是　　．（把所有正确结论的序号都选上）

如图， $\mathit{\Delta ABC}$ 中， $\mathit{AD}$ 是中线， $\mathit{BC}=8$ ， $\angle B=\angle \mathit{DAC}$ ，则线段 $\mathit{AC}$ 的长为 $($ 　　 $)$

A．

4

B．

$4\sqrt{2}$

C．

6

D．

$4\sqrt{3}$

如图，为的直径，为延长线上一点，是的切线，为切点，于点，交于点．

（1）求证：；

（2）若，，求的长．

如图，在平行四边形ABCD中，点E在AD上，连接CE并延长与BA的延长线交于点F，若AE=2ED，CD=3cm，则AF的长为（  ）

A．5cm

B．6cm

C．7cm

D．8cm

如图，在x轴的上方，直角∠BOA绕原点O按顺时针方向旋转，若∠BOA的两边分别与函数y=﹣、y=的图象交于B、A两点，则∠OAB的大小的变化趋势为（  ）

A．逐渐变小       B．逐渐变大       C．无法确定       D．保持不变

如图1，△ABC中，BC=25，BC边上的高为20，将AB，AC分别n等分，连接两边对应的等分点，以这些连接线为一边做矩形，使这些矩形的边B₁C₁,B₂C₂,B₃C₃……的对应边分别为 B₂C₂,B₃C₃,B₄C₄……

（1）若n=5，如图2，求B₃C₃为一边的矩形的面积；
（2）若n=5，求所有矩形的面积和；
（3）当分为n等分时，你能用含有n的表达式表示所有矩形的面积和吗？

如图，已知∠MON=90°，A是∠MON内部的一点，过点A作AB⊥ON，垂足为点B，AB=3厘米，OB=4厘米，动点E，F同时从O点出发，点E以1．5厘米/秒的速度沿ON方向运动，点F以2厘米/秒的速度沿OM方向运动，EF与OA交于点C，连接AE，当点E到达点B时，点F随之停止运动．设运动时间为t秒（t＞0）．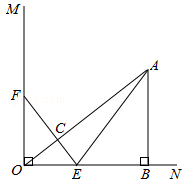

（1）当t=1秒时，△EOF与△ABO是否相似？请说明理由；
（2）在运动过程中，不论t取何值时，总有EF⊥OA．为什么？
（3）连接AF，在运动过程中，是否存在某一时刻t，使得S_△AEF=S_{四边形ABOF}？若存在，请求出此时t的值；若不存在，请说明理由．