如图,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.5米,A、B、C三点共线),把一面镜子水平放置在平台上的点G处,测得CG=15米,然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得EG=3米,小明身高1.6米,则凉亭的高度AB约为( )

A.8.5米B.9米C.9.5米D.10米
如图,一块材料的形状是锐角三角形 ,边 ,高 ,把它加工成正方形零件,使正方形的一边在 上,其余两个顶点分别在 、 上,这个正方形零件的边长是多少?
有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2等于( )

A.1: B.1:2C.2:3D.4:9
B.1:2C.2:3D.4:9
如图,在河对岸有一矩形场地 ,为了估测场地大小,在笔直的河岸 上依次取点 , , ,使 , ,点 , , 在同一直线上.在 点观测 点后,沿 方向走到 点,观测 点发现 .测得 米, 米, 米, ,则场地的边 为 米, 为 米.

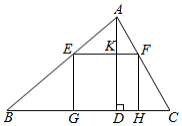
如图,在 中, ,高 ,正方形 一边在 上,点 , 分别在 , 上, 交 于点 ,则 的长为

| A. |
15 |
B. |
20 |
C. |
25 |
D. |
30 |
如图,在一斜边长 的直角三角形木板(即 中截取一个正方形 ,点 在边 上,点 在斜边 上,点 在边 上,若 ,则这块木板截取正方形 后,剩余部分的面积为

A. B. C. D.
小强的爸爸准备驾车外出.启动汽车时,车载报警系统显示正前方有障碍物,此时在眼睛点 处测得汽车前端 的俯角为 ,且 ,若直线 与地面 相交于点 ,点 到地面 的垂线段 的长度为1.6米,假设眼睛 处的水平线 与地面 平行.

(1)求 的长度;
(2)假如障碍物上的点 正好位于线段 的中点位置(障碍物的横截面为长方形,且线段 为此长方形前端的边), ,若小强的爸爸将汽车沿直线 后退0.6米,通过汽车的前端 点恰好看见障碍物的顶部 点(点 为点 的对应点,点 为点 的对应点),求障碍物的高度.
如图1, 为矩形 的边 上一点,点 从点 出发沿折线 运动到点 停止,点 从点 出发沿 运动到点 停止,它们运动的速度都是 .若点 、点 同时开始运动,设运动时间为 , 的面积为 ,已知 与 之间的函数图象如图2所示.
给出下列结论:①当 时, 是等腰三角形;② ;③当 时, ;④在运动过程中,使得 是等腰三角形的 点一共有3个;⑤ 与 相似时, .
其中正确结论的序号是 .

在平面直角坐标系中,已知抛物线经过点
和点
,
关于原点
对称的抛物线为
.
(1)求抛物线的表达式;
(2)点在抛物线
上,且位于第一象限,过点
作
轴,垂足为
.若
与
相似,求符合条件的点
的坐标.

如图,树 在路灯 的照射下形成投影 ,已知路灯高 ,树影 ,树 与路灯 的水平距离 ,则树的高度 长是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为 ,且三角板的一边长为 .则投影三角板的对应边长为

A. B. C. D.
为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理.她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端 ,标记好脚掌中心位置为 ,测得脚掌中心位置 到镜面中心 的距离是 ,镜面中心 距离旗杆底部 的距离为 ,如图所示.已知小丽同学的身高是 ,眼睛位置 距离小丽头顶的距离是 ,则旗杆 的高度等于

A. B. C. D.
如图,身高为1.8米的某学生想测量学校旗杆的高度,当他站在 处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得 米, 米,则旗杆 的高度是 米.

某市为了打造森林城市,树立城市新地标,实现绿色、共享发展理念,在城南建起了"望月阁"及环阁公园.小亮、小芳等同学想用一些测量工具和所学的几何知识测量"望月阁"的高度,来检验自己掌握知识和运用知识的能力.他们经过观察发现,观测点与"望月阁"底部间的距离不易测得,因此经过研究需要两次测量,于是他们首先用平面镜进行测量.方法如下:如图,小芳在小亮和"望月阁"之间的直线 上平放一平面镜,在镜面上做了一个标记,这个标记在直线 上的对应位置为点 ,镜子不动,小亮看着镜面上的标记,他来回走动,走到点 时,看到"望月阁"顶端点 在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地面的高度 米, 米,然后,在阳光下,他们用测影长的方法进行了第二次测量,方法如下:如图,小亮从 点沿 方向走了16米,到达"望月阁"影子的末端 点处,此时,测得小亮身高 的影长 米, 米.
如图,已知 , , ,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出"望月阁"的高 的长度.

试题篮
()