初中数学解直角三角形解答题

如图，在 $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{AC}$，以 $\mathit{AC}$边为直径作 $\odot O$交 $\mathit{BC}$边于点 $D$，过点 $D$作 $\mathit{DE}\perp \mathit{AB}$于点 $E$， $\mathit{ED}$、 $\mathit{AC}$的延长线交于点 $F$．

（1）求证： $\mathit{EF}$是 $\odot O$的切线；

（2）若 $\mathit{EB}=\frac{3}{2}$，且 $\sin \angle \mathit{CFD}=\frac{3}{5}$，求 $\odot O$的半径与线段 $\mathit{AE}$的长．

如图，已知 $\mathit{AB}$为半圆 $O$的直径， $C$为半圆 $O$上一点，连接 $\mathit{AC}$， $\mathit{BC}$，过点 $O$作 $\mathit{OD}\perp \mathit{AC}$于点 $D$，过点 $A$作半圆 $O$的切线交 $\mathit{OD}$的延长线于点 $E$，连接 $\mathit{BD}$并延长交 $\mathit{AE}$于点 $F$．

（1）求证： $\mathit{AE}·\mathit{BC}=\mathit{AD}·\mathit{AB}$；

（2）若半圆 $O$的直径为10， $\sin \angle \mathit{BAC}=\frac{3}{5}$，求 $\mathit{AF}$的长．

如图①， $\mathit{\Delta ABC}$中， $\angle \mathit{ABC}=45°$， $\mathit{AH}\perp \mathit{BC}$于点 $H$，点 $D$在 $\mathit{AH}$上，且 $\mathit{DH}=\mathit{CH}$，连接 $\mathit{BD}$．

（1）求证： $\mathit{BD}=\mathit{AC}$；

（2）将 $\mathit{\Delta BHD}$绕点 $H$旋转，得到 $\mathit{\Delta EHF}$（点 $B$， $D$分别与点 $E$， $F$对应），连接 $\mathit{AE}$．

①如图②，当点 $F$落在 $\mathit{AC}$上时， $(F$不与 $C$重合），若 $\mathit{BC}=4$， $\tan C=3$，求 $\mathit{AE}$的长；

②如图③，当 $\mathit{\Delta EHF}$是由 $\mathit{\Delta BHD}$绕点 $H$逆时针旋转 $30°$得到时，设射线 $\mathit{CF}$与 $\mathit{AE}$相交于点 $G$，连接 $\mathit{GH}$，试探究线段 $\mathit{GH}$与 $\mathit{EF}$之间满足的等量关系，并说明理由．

如图，在 $\text{Rt}\Delta \text{ABC}$中， $\angle \mathit{ABC}=90°$，以 $\mathit{CB}$为半径作 $\odot C$，交 $\mathit{AC}$于点 $D$，交 $\mathit{AC}$的延长线于点 $E$，连接 $\mathit{BD}$， $\mathit{BE}$．

（1）求证： $\mathit{\Delta ABD}\backsim \mathit{\Delta AEB}$；

（2）当 $\frac{\mathit{AB}}{\mathit{BC}}=\frac{4}{3}$时，求 $\tan E$；

（3）在（2）的条件下，作 $\angle \mathit{BAC}$的平分线，与 $\mathit{BE}$交于点 $F$，若 $\mathit{AF}=2$，求 $\odot C$的半径．

如图，在 $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{AC}$，以 $\mathit{AB}$为直径的 $\odot O$与边 $\mathit{BC}$， $\mathit{AC}$分别交于 $D$， $E$两点，过点 $D$作 $\mathit{DH}\perp \mathit{AC}$于点 $H$．

（1）判断 $\mathit{DH}$与 $\odot O$的位置关系，并说明理由；

（2）求证： $H$为 $\mathit{CE}$的中点；

（3）若 $\mathit{BC}=10$， $\cos C=\frac{\sqrt{5}}{5}$，求 $\mathit{AE}$的长．

已知：△ ABC内接于⊙ O， D是 $\stackrel{̂}{\mathit{BC}}$ 上一点， $\mathit{OD}\perp \mathit{BC}$ ，垂足为 H．

（1）如图1，当圆心 O在 AB边上时，求证： $\mathit{AC}＝2\mathit{OH}$ ；

（2）如图2，当圆心 O在△ ABC外部时，连接 AD、 CD， AD与 BC交于点 P，求证： $\angle \mathit{ACD}＝\angle \mathit{APB}$ ；

（3）在（2）的条件下，如图3，连接 BD， E为⊙ O上一点，连接 DE交 BC于点 Q、交 AB于点 N，连接 OE， BF为⊙ O的弦， $\mathit{BF}\perp \mathit{OE}$ 于点 R交 DE于点 G，若 $\angle \mathit{ACD}﹣\angle \mathit{ABD}＝2\angle \mathit{BDN}$ ， $\mathit{AC}=5\sqrt{5}$ ， $\mathit{BN}=3\sqrt{5}$ , $\mathrm{}\tan \angle \mathit{ABC}=\frac{1}{2}$ ,求 BF的长．

如图，⊙ O的直径 AB＝10，弦 AC＝8，连接 BC．

（1）尺规作图：作弦 CD，使 CD＝ BC（点 D不与 B重合），连接 AD；（保留作图痕迹，不写作法）

（2）在（1）所作的图中，求四边形 ABCD的周长．

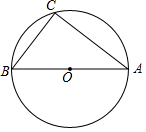
如图，△ ABC内接于⊙ O， BC＝2， AB＝ AC，点 D为 $\stackrel{⏜}{\mathit{AC}}$ 上的动点，且cos∠ ABC＝ $\frac{\sqrt{10}}{10}$ ．

（1）求 AB的长度；

（2）在点 D的运动过程中，弦 AD的延长线交 BC延长线于点 E，问 AD• AE的值是否变化？若不变，请求出 AD• AE的值；若变化，请说明理由；

（3）在点 D的运动过程中，过 A点作 AH⊥ BD，求证： BH＝ CD+ DH．

已知菱形的一个角与三角形的一个角重合，然后它的对角顶点在这个重合角的对边上，这个菱形称为这个三角形的亲密菱形，如图，在△ CFE中， CF＝6， CE＝12，∠ FCE＝45°，以点 C为圆心，以任意长为半径作 $\stackrel{⏜}{\mathit{AD}}$ ，再分别以点 A和点 D为圆心，大于 $\frac{1}{2}$ AD长为半径作弧，交 EF于点 B， AB∥ CD．

（1）求证：四边形 ACDB为△ FEC的亲密菱形；

（2）求四边形 ACDB的面积．

阅读下列材料：

如图1，在△ ABC中，∠ A、∠ B、∠ C所对的边分别为 a、 b、 c，可以得到：

S _{△ ABC}＝ $\frac{1}{2}$ absin C＝ $\frac{1}{2}$ acsin B＝ $\frac{1}{2}$ bcsin A

证明：过点 A作 AD⊥ BC，垂足为 D．

在Rt△ ABD中，sin B＝ $\frac{\mathit{AD}}{c}$

∴ AD＝ c•sin B

∴ S _{△ ABC}＝ $\frac{1}{2}$ a• AD＝ $\frac{1}{2}$ acsin B

同理： S _{△ ABC}＝ $\frac{1}{2}$ absin C

S _{△ ABC}＝ $\frac{1}{2}$ bcsin A

∴ S _{△ ABC}＝ $\frac{1}{2}$ absin C＝ $\frac{1}{2}$ acsin B＝ $\frac{1}{2}$ bcsin A

（1）通过上述材料证明：

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$

（2）运用（1）中的结论解决问题：

如图2，在△ ABC中，∠ B＝15°，∠ C＝60°， AB＝20 $\sqrt{3}$ ，求 AC的长度．

（3）如图3，为了开发公路旁的城市荒地，测量人员选择 A、 B、 C三个测量点，在 B点测得 A在北偏东75°方向上，沿笔直公路向正东方向行驶18 km到达 C点，测得 A在北偏西45°方向上，根据以上信息，求 A、 B、 C三点围成的三角形的面积．

（本题参考数值：sin15°≈0.3，sin120°≈0.9， $\sqrt{2}$ ≈1.4，结果取整数）

如图，在四边形 ABCD中， AD∥ BC，∠ ABC＝90°， AB＝ AD，连接 BD，点 E在 AB上，且∠ BDE＝15°， DE＝4 $\sqrt{3}$ ， DC＝2 $\sqrt{21}$ ．

（1）求 BE的长；

（2）求四边形 DEBC的面积．

（注意：本题中的计算过程和结果均保留根号）

阅读理解：

我们知道，四边形具有不稳定性，容易变形，如图1，一个矩形发生变形后成为一个平行四边形，设这个平行四边形相邻两个内角中较小的一个内角为α，我们把 $\frac{1}{\sin \alpha }$的值叫做这个平行四边形的变形度．

（1）若矩形发生变形后的平行四边形有一个内角是120度，则这个平行四边形的变形度是　　．

猜想证明：

（2）设矩形的面积为S₁，其变形后的平行四边形面积为S₂，试猜想S₁，S₂， $\frac{1}{\sin \alpha }$之间的数量关系，并说明理由；

拓展探究：

（3）如图2，在矩形ABCD中，E是AD边上的一点，且 $A{B}^2＝\mathit{AE}•\mathit{AD}$，这个矩形发生变形后为平行四边形A₁B₁C₁D₁，E₁为E的对应点，连接B₁E₁，B₁D₁，若矩形ABCD的面积为 $4\sqrt{\pi }(m>0)$，平行四边形A₁B₁C₁D₁的面积为 $2\sqrt{\pi }(m>0)$，试求∠A₁E₁B₁+∠A₁D₁B₁的度数．

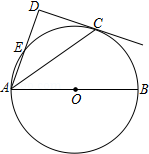
如图，点C在以AB为直径的⊙O上，AD与过点C的切线垂直，垂足为点D，AD交⊙O于点E．

（1）求证：AC平分 $\angle \mathit{DAB}$；

（2）连接BE交AC于点F，若 $\cos \angle \mathit{CAD}=\frac{4}{5}$，求 $\frac{\text{AF}}{\text{FC}}$的值．

如图，已知 AD是△ ABC的外角∠ EAC的平分线，交 BC的延长线于点 D，延长 DA交△ ABC的外接圆于点 F，连接 FB， FC．

（1）求证：∠ FBC＝∠ FCB；

（2）已知 FA• FD＝12，若 AB是△ ABC外接圆的直径， FA＝2，求 CD的长．

如图，△ ABC中， AD⊥ BC，垂足是 D，若 BC＝14， AD＝12，tan∠ BAD＝ $\frac{3}{4}$ ，求sin C的值．