如图, 是 的直径,点 为圆上一点, , 的平分线交 于点 , ,则 的直径为

| A. |
|
B. |
|
C. |
1 |
D. |
2 |
如图,在矩形 中, , ,点 , 分别是边 , 上的动点,点 不与 , 重合,且 , 是五边形 内满足 且 的点.现给出以下结论:
① 与 一定互补;
②点 到边 , 的距离一定相等;
③点 到边 , 的距离可能相等;
④点 到边 的距离的最大值为 .
其中正确的是 .(写出所有正确结论的序号)
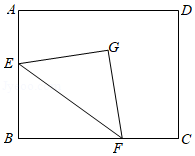
如图,在四边形 中, ,点 在 上, , ,垂足为 .
(1)求证:四边形 是平行四边形;
(2)若 平分 , , ,求 和 的长.
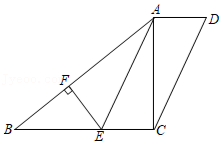
△ABC为等边三角形, , 于点D,E为线段 上一点, .以AE为边在直线 右侧构造等边三角形 ,连接 ,N为 的中点.
(1)如图1, 交于点G,连接 ,求线段 的长;
(2)如图2,将 绕点A逆时针旋转,旋转角为α,M为线段EF的中点,连接 , .当 时,猜想∠DNM的大小是否为定值,并证明你的结论;
(3)连接BN,在 绕点A逆时针旋转过程中,当线段BN最大时,请直接写出 的面积.

如图1,在 中, , , ,点D为AB的中点,线段 上有一动点E,连接DE,作DA关于直线DE的对称图形,得到 ,过点F作 于点G.设A、E两点间的距离为 , 两点间的距离为
小军根据学习函数的经验,对因变量y随自变量x的变化而变化的规律进行了探究.
下面是小军的探究过程,请补充完整.

(1)列表:如表的已知数据是根据A,E两点间的距离x进行取点、画图、测量,分别得到了x与y的几组对应值:
x/cm |
0 |
0.51 |
1.03 |
1.41 |
1.50 |
1.75 |
2.20 |
2.68 |
3.00 |
3.61 |
4.10 |
4.74 |
5.00 |
y/cm |
0 |
0.94 |
1.91 |
2.49 |
|
2.84 |
3.00 |
2.84 |
2.60 |
2.00 |
1.50 |
0.90 |
0.68 |
请你通过计算补全表格;
(2)描点、连线:在平面直角坐标系 中(如图2),描出表中各组数值所对应的点 ,并画出y关于x的图象;
(3)探究性质:随着x值的不断增大,y的值是怎样变化的? ;
(4)解决问题:当 时,FG的长度大约是 cm(保留两位小数).
如图,平面直角坐标系中,点 在第一象限,点 在 轴的正半轴上, , .将 绕点 逆时针旋转 ,点 的对应点 的坐标是

A. , B. C. , D.
如图,在 的正方形网格中,每个小正方形的边长都是1, 的顶点都在这些小正方形的顶点上,那么 的值为

A. B. C. D.
如图,在矩形 中, , .把 沿 折叠,使点 恰好落在 边上的 处,再将 绕点 顺时针旋转 ,得到△ ,使得 恰好经过 的中点 . 交 于点 ,连接 .有如下结论:① 的长度是 ;②弧 的长度是 ;③△ △ ;④△ .上述结论中,所有正确的序号是 .
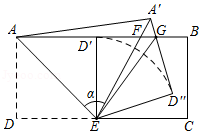
如图, , 为 上两点,且在直径 两侧,连结 交 于点 , 是 上一点, .
(1)求证: .
(2)点 关于 的对称点为 ,连结 .当点 落在直径 上时, , ,求 的半径.
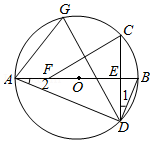
如图,在 中, ,以其三边为边向外作正方形,过点 作 于点 ,再过点 作 分别交边 , 于点 , .若 , ,则 的长为

A.14B.15C. D.
如图,菱形 的顶点 , , 在 上,过点 作 的切线交 的延长线于点 .若 的半径为1,则 的长为
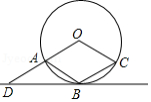
A.1B.2C. D.
试题篮
()