如图,在 中, , 是 的角平分线,点 在边 上.过点 、 的圆的圆心 在边 上,它与边 交于另一点 .
(1)试判断 与圆 的位置关系,并说明理由;
(2)若 , ,求 的长.

如图, 为 的直径, 为 上一点, 的平分线交 于点 , 于点 .
(1)试判断 与 的位置关系,并说明理由;
(2)过点 作 于点 ,若 , ,求图中阴影部分的面积.

如图, 中, , , ,将 绕点 顺时针旋转 得到△ , 为线段 上的动点, 以点 为圆心, 长为半径作 ,当 与 的边相切时, 的半径为 .
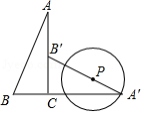
如图, 、 分别是 的直径和弦, 于点 .过点 作 的切线与 的延长线交于点 , 、 的延长线交于点 .
(1)求证: 是 的切线;
(2)若 , ,求线段 的长.
如图,矩形 的顶点 , 在 轴的正半轴上,反比例函数 在第一象限内的图象经过点 ,交 于点 .若 , , ,则 的值为

A.3B. C.6D.12
【定义】如图1, , 为直线 同侧的两点,过点 作直线 的对称点 ,连接 交直线 于点 ,连接 ,则称点 为点 , 关于直线 的“等角点”.
【运用】如图2,在平面直角坐标系 中,已知 , 两点.
(1) , , 三点中,点 是点 , 关于直线 的等角点;
(2)若直线 垂直于 轴,点 是点 , 关于直线 的等角点,其中 , ,求证: ;
(3)若点 是点 , 关于直线 的等角点,且点 位于直线 的右下方,当 时,求 的取值范围(直接写出结果).

结果如此巧合
下面是小颖对一道题目的解答.
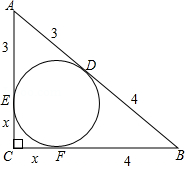
题目:如图, 的内切圆与斜边 相切于点 , , ,求 的面积.
解:设 的内切圆分别与 、 相切于点 、 , 的长为 .
根据切线长定理,得 , , .
根据勾股定理,得 .
整理,得 .
所以
.
小颖发现12恰好就是 ,即 的面积等于 与 的积.这仅仅是巧合吗?
请你帮她完成下面的探索.
已知: 的内切圆与 相切于点 , , .
可以一般化吗?
(1)若 ,求证: 的面积等于 .
倒过来思考呢?
(2)若 ,求证 .
改变一下条件
(3)若 ,用 、 表示 的面积.
如图,在平面直角坐标系中,一次函数 的图象与 轴和 轴分别相交于 、 两点.动点 从点 出发,在线段 上以每秒3个单位长度的速度向点 作匀速运动,到达点 停止运动,点 关于点 的对称点为点 ,以线段 为边向上作正方形 .设运动时间为 秒.
(1)当 秒时,点 的坐标是 ;
(2)在运动过程中,设正方形 与 重叠部分的面积为 ,求 与 的函数表达式;
(3)若正方形 对角线的交点为 ,请直接写出在运动过程中 的最小值.

在菱形 中, ,点 是射线 上一动点,以 为边向右侧作等边 ,点 的位置随着点 的位置变化而变化.

(1)如图1,当点 在菱形 内部或边上时,连接 , 与 的数量关系是 , 与 的位置关系是 ;
(2)当点 在菱形 外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由(选择图2,图3中的一种情况予以证明或说理);
(3)如图4,当点 在线段 的延长线上时,连接 ,若 , ,求四边形 的面积.
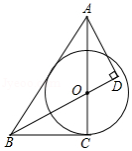
如图,在 中, 为 上一点,以点 为圆心, 为半径做圆,与 相切于点 ,过点 作 交 的延长线于点 ,且 .
(1)求证: 为 的切线;
(2)若 , ,求 的长.
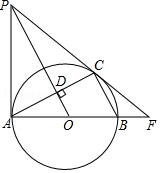
如图,已知 为锐角 内部一点,过点 作 于点 , 于点 ,以 为直径作 ,交直线 于点 ,连接 , , 交 于点 .
(1)求证: .
(2)连接 , ,当 , 时,在点 的整个运动过程中.
①若 ,求 的长.
②若 为等腰三角形,求所有满足条件的 的长.
(3)连接 , , 交 于点 ,当 , 时,记 的面积为 , 的面积为 ,请写出 的值.
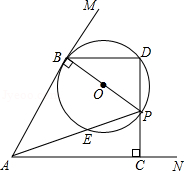
如图, 是 的 边上一点,连接 ,作 的外接圆,将 沿直线 折叠,点 的对应点 落在 上.
(1)求证: .
(2)若 , , ,求 的长.

如图1,直线 与 轴交于点 ,与 轴交于点 ,点 是线段 上一动点 .以点 为圆心, 长为半径作 交 轴于另一点 ,交线段 于点 ,连接 并延长交 于点 .

(1)求直线 的函数表达式和 的值;
(2)如图2,连接 ,当 时,
①求证: ;
②求点 的坐标;
(3)当点 在线段 上运动时,求 的最大值.
在 中, , .点 在直线 上,以 , 为边作矩形 ,直线 与直线 , 的交点分别为 , .
(1)如图,点 在线段 上,四边形 是正方形.
①若点 为 的中点,求 的长.
②若 ,求 的长.
(2)已知 ,是否存在点 ,使得 是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.

试题篮
()