图1是太阳能热水器装置的示意图.利用玻璃吸热管可以把太阳能转化为热能,玻璃吸热管与太阳光线垂直时,吸收太阳能的效果最好,假设某用户要求根据本地区冬至正午时刻太阳光线与地面水平线的夹角 确定玻璃吸热管的倾斜角(太阳光线与玻璃吸热管垂直),请完成以下计算:
如图2, ,垂足为点 , ,垂足为点 , , , , ,垂足为点 .
(1)若 ,则 的长约为 ;
(参考数据: , ,
(2)若 , ,求 的长.

如图,三条笔直公路两两相交,交点分别为、
、
,测得
,
,
千米,求
、
两点间的距离.(参考数据:
,
,结果精确到1千米).

如图, , 两点被池塘隔开,在 外选一点 ,连接 , .测得 , , .根据测得的数据,求 的长(结果取整数).
参考数据: , , .

小华同学将笔记本电脑水平放置在桌子上,当显示屏的边缘线 与底板的边缘线 所在水平线的夹角为 时,感觉最舒适(如图① .侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点 、 、 在同一直线上, , , .

(1)求 的长;
(2)如图④,垫入散热架后,要使显示屏的边缘线 与水平线的夹角仍保持 ,求点 到 的距离.(结果保留根号)
如图所示,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路 的 处,测得一辆汽车从 处行驶到 处所用时间为0.9秒,已知 , .
(1)求 , 之间的距离;(保留根号)
(2)如果此地限速为 ,那么这辆汽车是否超速?请说明理由.(参考数据: ,

如图,为了测量河对岸两点 , 之间的距离,在河岸这边取点 , .测得 , , , , .设 , , , 在同一平面内,求 , 两点之间的距离.
(参考数据: , .

图1是第七届国际数学教育大会 会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形 .若 , ,则 的值为
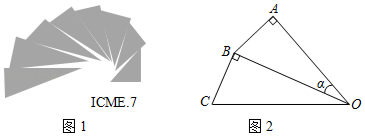
| A. |
|
B. |
|
C. |
|
D. |
|
拓展小组研制的智能操作机器人,如图1,水平操作台为 ,底座 固定,高 为 ,连杆 长度为 ,手臂 长度为 .点 , 是转动点,且 , 与 始终在同一平面内.
(1)转动连杆 ,手臂 ,使 , ,如图2,求手臂端点 离操作台 的高度 的长(精确到 ,参考数据: , .
(2)物品在操作台 上,距离底座 端 的点 处,转动连杆 ,手臂 ,手臂端点 能否碰到点 ?请说明理由.

2021年,达州河边新建成了一座美丽的大桥.某学校数学兴趣小组组织了一次测桥墩高度的活动,如图,桥墩刚好在坡角为 的河床斜坡边,斜坡 长为48米,在点 处测得桥墩最高点 的仰角为 , 平行于水平线 , 长为 米,求桥墩 的高(结果保留1位小数). , , ,

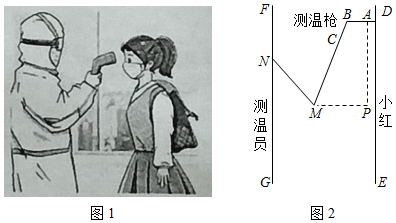
图1是疫情期间测温员用"额温枪"对小红测温时的实景图,图2是其侧面示意图,其中枪柄 与手臂 始终在同一直线上,枪身 与额头保持垂直.量得胳膊 , ,肘关节 与枪身端点 之间的水平宽度为 (即 的长度),枪身 .
(1)求 的度数;
(2)测温时规定枪身端点 与额头距离范围为 .在图2中,若测得 ,小红与测温员之间距离为 .问此时枪身端点 与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)
(参考数据: , , ,
有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.图2是这种升降熨烫台的平面示意图. 和 是两根相同长度的活动支撑杆,点 是它们的连接点, , 表示熨烫台的高度.
(1)如图 .若 , ,求 的值;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度为 时,两根支撑杆的夹角 是 (如图 .求该熨烫台支撑杆 的长度(结果精确到 .
(参考数据: , , ,

试题篮
()