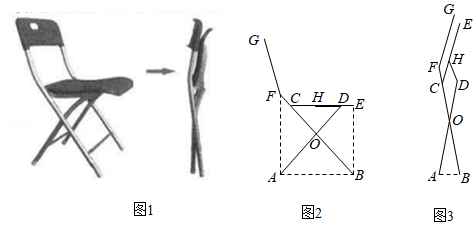
图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面 与地面平行,支撑杆 , 可绕连接点 转动,且 ,椅面底部有一根可以绕点 转动的连杆 ,点 是 的中点, , 均与地面垂直,测得 , , .
(1)椅面 的长度为 .
(2)如图3,椅子折叠时,连杆 绕着支点 带动支撑杆 , 转动合拢,椅面和连杆夹角 的度数达到最小值 时, , 两点间的距离为 (结果精确到 .
(参考数据: , ,
已知的直径
,弦
与弦
交于点
.且
,垂足为点
.

(1)如图1,如果,求弦
的长;
(2)如图2,如果为弦
的中点,求
的余切值;
(3)联结、
、
,如果
是
的内接正
边形的一边,
是
的内接正
边形的一边,求
的面积.
某镇为创建特色小镇,助力乡村振兴,决定在辖区的一条河上修建一座步行观光桥.如图,该河旁有一座小山,山高 ,坡面 的坡度 (注:坡度 是指坡面的铅直高度与水平宽度的比),点 、 与河岸 、 在同一水平线上,从山顶 处测得河岸 和对岸 的俯角分别为 , .
(1)求山脚 到河岸 的距离;
(2)若在此处建桥,试求河宽 的长度.(结果精确到
(参考数据: , ,
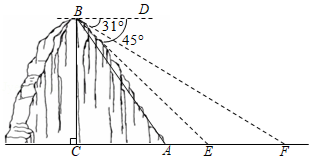
如图,点 为正六边形 对角线 上一点, , ,则 的值是

| A. |
20 |
B. |
30 |
| C. |
40 |
D. |
随点 位置而变化 |
某种落地灯如图1所示, 为立杆,其高为 ; 为支杆,它可绕点 旋转,其中 长为 ; 为悬杆,滑动悬杆可调节 的长度.支杆 与悬杆 之间的夹角 为 .
(1)如图2,当支杆 与地面垂直,且 的长为 时,求灯泡悬挂点 距离地面的高度;
(2)在图2所示的状态下,将支杆 绕点 顺时针旋转 ,同时调节 的长(如图 ,此时测得灯泡悬挂点 到地面的距离为 ,求 的长.(结果精确到 ,参考数据: , , , , ,

2021年,达州河边新建成了一座美丽的大桥.某学校数学兴趣小组组织了一次测桥墩高度的活动,如图,桥墩刚好在坡角为 的河床斜坡边,斜坡 长为48米,在点 处测得桥墩最高点 的仰角为 , 平行于水平线 , 长为 米,求桥墩 的高(结果保留1位小数). , , ,

一座吊桥的钢索立柱 两侧各有若干条斜拉的钢索,大致如图所示.小明和小亮想用测量知识测较长钢索 的长度.他们测得 为 ,由于 、 两点间的距离不易测得,通过探究和测量,发现 恰好为 ,点 与点 之间的距离约为 .已知 、 、 共线, .求钢索 的长度.(结果保留根号)

某公园为引导游客观光游览公园的景点,在主要路口设置了导览指示牌,某校"综合与实践"活动小组想要测量此指示牌的高度,他们绘制了该指示牌支架侧面的截面图如图所示,并测得 , , , ,四边形 为矩形,且 .请帮助该小组求出指示牌最高点 到地面 的距离(结果精确到 .参考数据: , , , .

图1是放置在水平地面上的落地式话筒架实物图,图2是其示意图.支撑杆 垂直于地面 ,活动杆 固定在支撑杆上的点 处.若 , , ,求活动杆端点 离地面的高度 .(结果精确到 ,参考数据: , ,
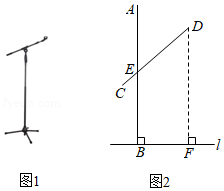
我国纸伞的制作工艺十分巧妙.如图1,伞不管是张开还是收拢,伞柄 始终平分同一平面内两条伞骨所成的角 ,且 ,从而保证伞圈 能沿着伞柄滑动.如图2是伞完全收拢时伞骨的示意图,此时伞圈 已滑动到点 的位置,且 , , 三点共线, , 为 中点.当 时,伞完全张开.
(1)求 的长.
(2)当伞从完全张开到完全收拢,求伞圈 沿着伞柄向下滑动的距离.
(参考数据: , ,

如图,为了测量某建筑物 的高度,小颖采用了如下的方法:先从与建筑物底端 在同一水平线上的 点出发,沿斜坡 行走130米至坡顶 处,再从 处沿水平方向继续前行若干米后至点 处,在 点测得该建筑物顶端 的仰角为 ,建筑物底端 的俯角为 ,点 、 、 、 、 在同一平面内,斜坡 的坡度 .根据小颖的测量数据,计算出建筑物 的高度约为(参考数据:

| A. |
136.6米 |
B. |
86.7米 |
C. |
186.7米 |
D. |
86.6米 |
如图,在某小区内拐角处的一段道路上,有一儿童在 处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的 处驶来,已知 , , , ,汽车从 处前行多少米才能发现 处的儿童(结果保留整数)?
(参考数据: , , ; , ,

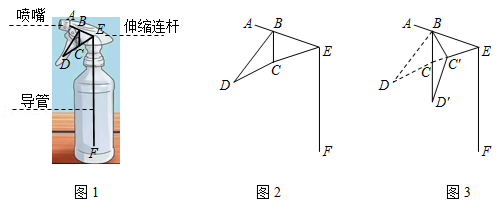
一酒精消毒瓶如图1, 为喷嘴, 为按压柄, 为伸缩连杆, 和 为导管,其示意图如图2, , , .当按压柄 按压到底时, 转动到 ,此时 (如图 .
(1)求点 转动到点 的路径长;
(2)求点 到直线 的距离(结果精确到 .
(参考数据: , , , , ,
如图1是某中学教学楼的推拉门,已知门的宽度 米,且两扇门的大小相同(即 ,将左边的门 绕门轴 向里面旋转 ,将右边的门 绕门轴 向外面旋转 ,其示意图如图2,求此时 与 之间的距离(结果保留一位小数).(参考数据: , ,

试题篮
()