图1是一商场的推拉门,已知门的宽度 米,且两扇门的大小相同(即 ,将左边的门 绕门轴 向里面旋转 ,将右边的门 绕门轴 向外面旋转 ,其示意图如图2,求此时 与 之间的距离(结果保留一位小数).(参考数据: , ,

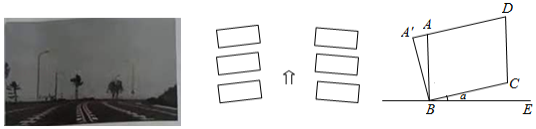
高速公路上有一种标线叫纵向减速标线,外号叫鱼骨线,作用是为了提醒驾驶员在开车时减速慢行.如图,用平行四边形 表示一个"鱼骨", 平行于车辆前行方向, , ,过 作 的垂线,垂足为 点的视觉错觉点),若 , ,则 .
问题背景:已知 的顶点 在 的边 所在直线上(不与 , 重合), 交 所在直线于点 , 交 所在直线于点 ,记 的面积为 , 的面积为 .
(1)初步尝试:如图①,当 是等边三角形, , ,且 , 时,则 ;
(2)类比探究:在(1)的条件下,先将点 沿 平移,使 ,再将 绕点 旋转至如图②所示位置,求 的值;
(3)延伸拓展:当 是等腰三角形时,设 .
(Ⅰ)如图③,当点 在线段 上运动时,设 , ,求 的表达式(结果用 , 和 的三角函数表示).
(Ⅱ)如图④,当点 在 的延长线上运动时,设 , ,直接写出 的表达式,不必写出解答过程.

如图,两根竹竿 和 斜靠在墙 上,量得 , ,则竹竿 与 的长度之比为

A. B. C. D.
如图,电线杆 的高度为 ,两根拉线 与 相互垂直, ,则拉线 的长度为 、 、 在同一条直线上)

A. B. C. D.
如图,为了测量某建筑物 的高度,小颖采用了如下的方法:先从与建筑物底端 在同一水平线上的 点出发,沿斜坡 行走130米至坡顶 处,再从 处沿水平方向继续前行若干米后至点 处,在 点测得该建筑物顶端 的仰角为 ,建筑物底端 的俯角为 ,点 、 、 、 、 在同一平面内,斜坡 的坡度 .根据小颖的测量数据,计算出建筑物 的高度约为(参考数据:

| A. |
136.6米 |
B. |
86.7米 |
C. |
186.7米 |
D. |
86.6米 |
如图1,2分别是某款篮球架的实物图与示意图,已知底座 米,底座 与支架 所成的角 ,支架 的长为2.50米,篮板顶端 点到篮筐 的距离 米,篮板底部支架 与支架 所成的角 ,求篮筐 到地面的距离(精确到0.01米)(参考数据: , , , ,

如图,一名滑雪运动员沿着倾斜角为 的斜坡,从 滑行至 ,已知 米,则这名滑雪运动员的高度下降了 米.(参考数据: , ,

为进一步加强疫情防控工作,避免在测温过程中出现人员聚集现象,某学校决定安装,该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温,无需人员停留和接触,安装说明书的部分内容如表.
名称 |
红外线体温检测仪 |
安装示意图 |
|
技术参数 |
探测最大角: |
探测最小角: |
|
安装要求 |
本设备需安装在垂直于水平地面AC的支架CP上 |
根据以上内容,解决问题:
学校要求测温区域的宽度AB为4m,请你帮助学校确定该设备的安装高度OC.
(结果精确到0.1m,参考数据: ,t , , , )
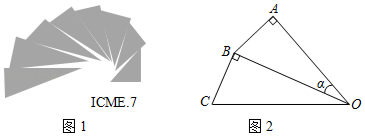
图1是第七届国际数学教育大会 会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形 .若 , ,则 的值为
| A. |
|
B. |
|
C. |
|
D. |
|
拓展小组研制的智能操作机器人,如图1,水平操作台为 ,底座 固定,高 为 ,连杆 长度为 ,手臂 长度为 .点 , 是转动点,且 , 与 始终在同一平面内.
(1)转动连杆 ,手臂 ,使 , ,如图2,求手臂端点 离操作台 的高度 的长(精确到 ,参考数据: , .
(2)物品在操作台 上,距离底座 端 的点 处,转动连杆 ,手臂 ,手臂端点 能否碰到点 ?请说明理由.

2021年,达州河边新建成了一座美丽的大桥.某学校数学兴趣小组组织了一次测桥墩高度的活动,如图,桥墩刚好在坡角为 的河床斜坡边,斜坡 长为48米,在点 处测得桥墩最高点 的仰角为 , 平行于水平线 , 长为 米,求桥墩 的高(结果保留1位小数). , , ,

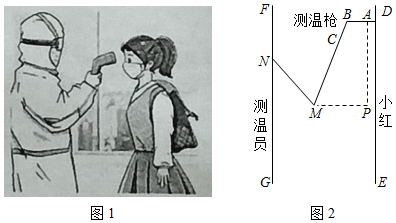
图1是疫情期间测温员用"额温枪"对小红测温时的实景图,图2是其侧面示意图,其中枪柄 与手臂 始终在同一直线上,枪身 与额头保持垂直.量得胳膊 , ,肘关节 与枪身端点 之间的水平宽度为 (即 的长度),枪身 .
(1)求 的度数;
(2)测温时规定枪身端点 与额头距离范围为 .在图2中,若测得 ,小红与测温员之间距离为 .问此时枪身端点 与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)
(参考数据: , , ,
有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.图2是这种升降熨烫台的平面示意图. 和 是两根相同长度的活动支撑杆,点 是它们的连接点, , 表示熨烫台的高度.
(1)如图 .若 , ,求 的值;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度为 时,两根支撑杆的夹角 是 (如图 .求该熨烫台支撑杆 的长度(结果精确到 .
(参考数据: , , ,

试题篮
()