初中数学解直角三角形的应用试题

图1是挂墙式淋浴花洒的实物图，图2是抽象出来的几何图形．为使身高 $175\mathit{cm}$ 的人能方便地淋浴，应当使旋转头固定在墙上的某个位置 $O$ ，花洒的最高点 $B$ 与人的头顶的铅垂距离为 $15\mathit{cm}$ ，已知龙头手柄 $\mathit{OA}$ 长为 $10\mathit{cm}$ ，花洒直径 $\mathit{AB}$ 是 $8\mathit{cm}$ ，龙头手柄与墙面的较小夹角 $\angle \mathit{COA}=26°$ ， $\angle \mathit{OAB}=146°$ ，则安装时，旋转头的固定点 $O$ 与地面的距离应为多少？（计算结果精确到 $1\mathit{cm}$ ，参考数据： $\sin 26°\approx 0.44$ ， $\cos 26°\approx 0.90$ ， $\tan 26°\approx 0.49)$

图1是某种路灯的实物图片，图2是该路灯的平面示意图， $\mathit{MN}$ 为立柱的一部分，灯臂 $\mathit{AC}$ ，支架 $\mathit{BC}$ 与立柱 $\mathit{MN}$ 分别交于 $A$ ， $B$ 两点，灯臂 $\mathit{AC}$ 与支架 $\mathit{BC}$ 交于点 $C$ ，已知 $\angle \mathit{MAC}=60°$ ， $\angle \mathit{ACB}=15°$ ， $\mathit{AC}=40\mathit{cm}$ ，求支架 $\mathit{BC}$ 的长．（结果精确到 $1\mathit{cm}$ ，参考数据： $\sqrt{2}\approx 1.414$ ， $\sqrt{3}\approx 1.732$ ， $\sqrt{6}\approx 2.449)$

筒车是我国古代利用水力驱动的灌溉工具，唐代陈廷章在《水轮赋）中写道：“水能利物，轮乃曲成”．如图，半径为的筒车按逆时针方向每分钟转圈，筒车与水面分别交于点、，筒车的轴心距离水面的高度长为，筒车上均匀分布着若干个盛水筒．若以某个盛水筒刚浮出水面时开始计算时间．

（1）经过多长时间，盛水筒首次到达最高点？

（2）浮出水面3.4秒后，盛水筒距离水面多高？

（3）若接水槽所在直线是的切线，且与直线交于点，．求盛水筒从最高点开始，至少经过多长时间恰好在直线上．

（参考数据：，，

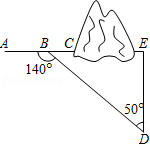
如图，三条笔直公路两两相交，交点分别为、、，测得，，千米，求、两点间的距离．（参考数据：，，结果精确到1千米）．

某高速公路管理部门工作人员在对某段高速公路进行安全巡检过程中，发现该高速公路旁的一斜坡存在落石隐患．该斜坡横断面示意图如图所示，水平线，点、分别在、上，斜坡的长为18米，过点作于点，且线段的长为米．

（1）求该斜坡的坡高；（结果用最简根式表示）

（2）为降低落石风险，该管理部门计划对该斜坡进行改造，改造后的斜坡坡角为，过点作于点，求改造后的斜坡长度比改造前的斜坡长度增加了多少米？

小华同学将笔记本电脑水平放置在桌子上，当显示屏的边缘线 $\mathit{OB}$ 与底板的边缘线 $\mathit{OA}$ 所在水平线的夹角为 $120°$ 时，感觉最舒适（如图① $)$ ．侧面示意图为图②；使用时为了散热，他在底板下面垫入散热架，如图③，点 $B$ 、 $O$ 、 $C$ 在同一直线上， $\mathit{OA}=\mathit{OB}=24\mathit{cm}$ ， $\mathit{BC}\perp \mathit{AC}$ ， $\angle \mathit{OAC}=30°$ ．

（1）求 $\mathit{OC}$ 的长；

（2）如图④，垫入散热架后，要使显示屏的边缘线 $O{B}^{\text{'}}$ 与水平线的夹角仍保持 $120°$ ，求点 $B\text{'}$ 到 $\mathit{AC}$ 的距离．（结果保留根号）

如图1是自动卸货汽车卸货时的状态图，图2是其示意图．汽车的车厢采用液压机构、车厢的支撑顶杆 $\mathit{BC}$ 的底部支撑点 $B$ 在水平线 $\mathit{AD}$ 的下方， $\mathit{AB}$ 与水平线 $\mathit{AD}$ 之间的夹角是 $5°$ ，卸货时，车厢与水平线 $\mathit{AD}$ 成 $60°$ ，此时 $\mathit{AB}$ 与支撑顶杆 $\mathit{BC}$ 的夹角为 $45°$ ，若 $\mathit{AC}=2$ 米，求 $\mathit{BC}$ 的长度．（结果保留一位小数）

（参考数据： $\sin 65°\approx 0.91$ ， $\cos 65°\approx 0.42$ ， $\tan 65°\approx 2.14$ ， $\sin 70°\approx 0.94$ ， $\cos 70°\approx 0.34$ ， $\tan 70°\approx 2.75$ ， $\sqrt{2}\approx 1.41)$

某型号飞机的机翼形状如图所示，根据图中数据计算的长为　　．（结果保留根号）

襄阳东站的建成运营标志着我市正式进入高铁时代，郑万高速铁路襄阳至万州段的建设也正在推进中．如图，工程队拟沿 $\mathit{AC}$ 方向开山修路，为加快施工进度，需在小山的另一边点 $E$ 处同时施工．要使 $A$ 、 $C$ 、 $E$ 三点在一条直线上，工程队从 $\mathit{AC}$ 上的一点 $B$ 取 $\angle \mathit{ABD}=140°$ ， $\mathit{BD}=560$ 米， $\angle D=50°$ ．那么点 $E$ 与点 $D$ 间的距离是多少米？

（参考数据： $\sin 50°\approx 0.77$ ， $\cos 50°\approx 0.64$ ， $\tan 50°\approx 1.19)$

如图，要想使人安全地攀上斜靠在墙面上的梯子的顶端，梯子与地面所成的角 $\alpha$ 一般要满足 $50°⩽\alpha ⩽75°$ ，现有一架长为 $6m$ 的梯子，当梯子底端离墙面 $2m$ 时，此时人是否能够安全使用这架梯子（参考数据： $\sin 50°\approx 0.77$ ， $\cos 50°\approx 0.64$ ， $\sin 75°\approx 0.97$ ， $\cos 75°=0.26)$ ？

“健康荆州，你我同行”，市民小张积极响应“全民健身动起来”号召，坚持在某环形步道上跑步．已知此步道外形近似于如图所示的，其中，与间另有步道相连，地在正中位置，地与地相距．若，，小张某天沿路线跑一圈，则他跑了　　．

构建几何图形解决代数问题是"数形结合"思想的重要性，在计算 $\tan 15°$ 时，如图．在 $\text{Rt}\Delta \text{ACB}$ 中， $\angle C=90°$ ， $\angle \mathit{ABC}=30°$ ，延长 $\mathit{CB}$ 使 $\mathit{BD}=\mathit{AB}$ ，连接 $\mathit{AD}$ ，得 $\angle D=15°$ ，所以 $\tan 15°=\frac{\mathit{AC}}{\mathit{CD}}=\frac{1}{2+\sqrt{3}}=\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}=2-\sqrt{3}$ ．类比这种方法，计算 $\tan 22.5°$ 的值为 $($ 　　 $)$

A．

$\sqrt{2}+1$

B．

$\sqrt{2}-1$

C．

$\sqrt{2}$

D．

$\frac{1}{2}$

如图，某停车场入口的栏杆 $\mathit{AB}$ ，从水平位置绕点 $O$ 旋转到 $A\text{'}B\text{'}$ 的位置，已知 $\mathit{AO}$ 的长为4米．若栏杆的旋转角 $\angle \mathit{AOA}\text{'}=\alpha$ ，则栏杆 $A$ 端升高的高度为 $($ 　　 $)$

A．

$\frac{4}{\sin \alpha }$ 米

B．

$4\sin \alpha$ 米

C．

$\frac{4}{\cos \alpha }$ 米

D．

$4\cos \alpha$ 米

图①是甘肃省博物馆的镇馆之宝铜奔马，又称“马踏飞燕”，于1969年10月出土于武威市的雷台汉墓，1983年10月被国家旅游局确定为中国旅游标志．在很多旅游城市的广场上都有“马踏飞燕”雕塑．某学习小组把测量本城市广场的“马踏飞燕”雕塑（图②最高点离地面的高度作为一次课题活动，同学们制定了测量方案，并完成了实地测量，测得结果如下表：

课题	测量“马踏飞燕“雕塑最高点离地面的高度
测量示意图				如图，雕塑的最高点到地面的高度为，在测点用仪器测得点的仰角为，前进一段距离到达测点，再用该仪器测得点的仰角为，且点，，，，，均在同一竖直平面内，点，，在同一条直线上．
测量数据	的度数	的度数	的长度		仪器的高度
			5米		1.5米

请你根据上表中的测量数据，帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度（结果保留一位小数）．（参考数据：，，，，，

如图所示，九（1）班数学课外活动小组在河边测量河宽（这段河流的两岸平行），他们在点测得，点处测得，，则河宽约为　　（结果保留整数，．