某限高曲臂道路闸口如图所示, 垂直地面 于点 , 与水平线 的夹角为 , ,若 米, 米,车辆的高度为 (单位:米),不考虑闸口与车辆的宽度:
①当 时, 小于3.3米的车辆均可以通过该闸口;
②当 时, 等于2.9米的车辆不可以通过该闸口;
③当 时, 等于3.1米的车辆不可以通过该闸口.
则上述说法正确的个数为

| A. |
0个 |
B. |
1个 |
C. |
2个 |
D. |
3个 |
我国纸伞的制作工艺十分巧妙.如图1,伞不管是张开还是收拢,伞柄 始终平分同一平面内两条伞骨所成的角 ,且 ,从而保证伞圈 能沿着伞柄滑动.如图2是伞完全收拢时伞骨的示意图,此时伞圈 已滑动到点 的位置,且 , , 三点共线, , 为 中点.当 时,伞完全张开.
(1)求 的长.
(2)当伞从完全张开到完全收拢,求伞圈 沿着伞柄向下滑动的距离.
(参考数据: , ,

已知锐角 中,角 、 、 的对边分别为 、 、 ,边角总满足关系式: .

(1)如图1,若 , , ,求 的值;
(2)某公园准备在园内一个锐角三角形水池 中建一座小型景观桥 (如图2所示),若 , 米, 米, ,求景观桥 的长度.
如图,著名旅游景区 位于大山深处,原来到此旅游需要绕行 地,沿折线 方可到达.当地政府为了增强景区的吸引力,发展壮大旅游经济,修建了一条从 地到景区 的笔直公路.请结合 , , 千米, , 等数据信息,解答下列问题:
(1)公路修建后,从 地到景区 旅游可以少走多少千米?
(2)为迎接旅游旺季的到来,修建公路时,施工队使用了新的施工技术,实际工作时每天的工效比原计划增加 ,结果提前50天完成了施工任务.求施工队原计划每天修建多少千米?

如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为 时,梯子顶端靠在墙面上的点 处,底端落在水平地面的点 处,现将梯子底端向墙面靠近,使梯子与地面所成角为 ,已知 ,则梯子顶端上升了

| A. |
1米 |
B. |
1.5米 |
C. |
2米 |
D. |
2.5米 |
如图,在某小区内拐角处的一段道路上,有一儿童在 处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的 处驶来,已知 , , , ,汽车从 处前行多少米才能发现 处的儿童(结果保留整数)?
(参考数据: , , ; , ,

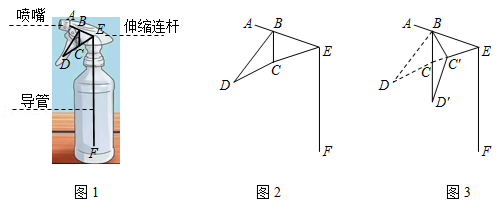
一酒精消毒瓶如图1, 为喷嘴, 为按压柄, 为伸缩连杆, 和 为导管,其示意图如图2, , , .当按压柄 按压到底时, 转动到 ,此时 (如图 .
(1)求点 转动到点 的路径长;
(2)求点 到直线 的距离(结果精确到 .
(参考数据: , , , , ,
如图1是某中学教学楼的推拉门,已知门的宽度 米,且两扇门的大小相同(即 ,将左边的门 绕门轴 向里面旋转 ,将右边的门 绕门轴 向外面旋转 ,其示意图如图2,求此时 与 之间的距离(结果保留一位小数).(参考数据: , ,

拓展小组研制的智能操作机器人,如图1,水平操作台为 ,底座 固定,高 为 ,连杆 长度为 ,手臂 长度为 .点 , 是转动点,且 , 与 始终在同一平面内.
(1)转动连杆 ,手臂 ,使 , ,如图2,求手臂端点 离操作台 的高度 的长(精确到 ,参考数据: , .
(2)物品在操作台 上,距离底座 端 的点 处,转动连杆 ,手臂 ,手臂端点 能否碰到点 ?请说明理由.

某工程队准备从 到 修建一条隧道,测量员在直线 的同一侧选定 , 两个观测点,如图.测得 长为 , 长为 , 长为 , , 、 、 、 在同一水平面内).
(1)求 、 两点之间的距离;
(2)求隧道 的长度.

今年疫情期间,针对各种入口处人工测量体温存在的感染风险高、效率低等问题,清华大学牵头研制一款“测温机器人”,如图1,机器人工作时,行人抬手在测温头处测量手腕温度,体温合格则机器人抬起臂杆行人可通行,不合格时机器人不抬臂杆并报警,从而有效阻隔病原体.

(1)为了设计“测温机器人”的高度,科研团队采集了大量数据.下表是抽样采集某一地区居民的身高数据:
测量对象 |
男性 岁) |
女性 岁) |
|||||
抽样人数(人 |
2000 |
5000 |
20000 |
2000 |
5000 |
20000 |
|
平均身高(厘米) |
173 |
175 |
176 |
164 |
165 |
164 |
|
根据你所学的知识,若要更准确的表示这一地区男、女的平均身高,男性应采用 176 厘米,女性应采用 厘米;
(2)如图2,一般的,人抬手的高度与身高之比为黄金比时给人的感觉最舒适,由此利用(1)中的数据得出测温头点 距地面105厘米.指示牌挂在两臂杆 , 的连接点 处, 点距地面110厘米.臂杆落下时两端点 , 在同一水平线上, 厘米,点 在点 的正下方5厘米处.若两臂杆长度相等,求两臂杆的夹角.
(参考数据表)
计算器按键顺序 |
计算结果(近似值) |
计算器按键顺序 |
计算结果(近似值) |
|
0.1 |
|
78.7 |
|
0.2 |
|
84.3 |
|
1.7 |
|
5.7 |
|
3.5 |
|
11.3 |
人字梯为现代家庭常用的工具(如图).若 , 的长都为 ,当 时,人字梯顶端离地面的高度 是 .(结果精确到 ,参考依据: , ,

图1是第七届国际数学教育大会 会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形 .若 , ,则 的值为
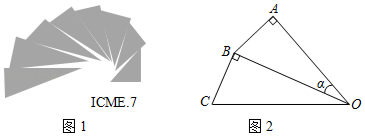
| A. |
|
B. |
|
C. |
|
D. |
|
图①、图②分别是某种型号跑步机的实物图与示意图.已知跑步机手柄 AB与地面 DE平行,踏板 CD长为1.5 m, CD与地面 DE的夹角 ,支架 AC长为1 m, ,求跑步机手柄 AB所在直线与地面 DE之间的距离.(结果精确到0.1 m.参考数据: , , , )

试题篮
()