初中数学解直角三角形的应用-方向角问题解答题

如图， $A$， $B$是海面上位于东西方向的两个观测点，有一艘海轮在 $C$点处遇险发出求救信号，此时测得 $C$点位于观测点 $A$的北偏东 $45°$方向上，同时位于观测点 $B$的北偏西 $60°$方向上，且测得 $C$点与观测点 $A$的距离为 $25\sqrt{2}$海里．

（1）求观测点 $B$与 $C$点之间的距离；

（2）有一艘救援船位于观测点 $B$的正南方向且与观测点 $B$相距30海里的 $D$点处，在接到海轮的求救信号后立即前往营救，其航行速度为42海里 $/$小时，求救援船到达 $C$点需要的最少时间．

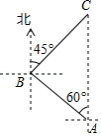
一名徒步爱好者来衡阳旅行，他从宾馆 $C$出发，沿北偏东 $30°$的方向行走2000米到达石鼓书院 $A$处，参观后又从 $A$处沿正南方向行走一段距离，到达位于宾馆南偏东 $45°$方向的雁峰公园 $B$处，如图所示．

（1）求这名徒步爱好者从石鼓书院走到雁峰公园的途中与宾馆之间的最短距离；

（2）若这名徒步爱好者以100米 $/$分的速度从雁峰公园返回宾馆，那么他在15分钟内能否到达宾馆？

科技改变生活，手机导航极大方便了人们的出行，如图，小明一家自驾到古镇 $C$游玩，到达 $A$地后，导航显示车辆应沿北偏西 $60°$方向行驶4千米至 $B$地，再沿北偏东 $45°$方向行驶一段距离到达古镇 $C$，小明发现古镇 $C$恰好在 $A$地的正北方向，求 $B$， $C$两地的距离．

如图所示， $C$城市在 $A$城市正东方向，现计划在 $A$、 $C$两城市间修建一条高速公路（即线段 $\mathit{AC})$，经测量，森林保护区的中心 $P$在 $A$城市的北偏东 $60°$方向上，在线段 $\mathit{AC}$上距 $A$城市 $120\mathit{km}$的 $B$处测得 $P$在北偏东 $30°$方向上，已知森林保护区是以点 $P$为圆心， $100\mathit{km}$为半径的圆形区域，请问计划修建的这条高速公路是否穿越保护区，为什么？（参考数据： $\sqrt{3}\approx 1.73)$

如图，一艘货船在灯塔 $C$ 的正南方向，距离灯塔257海里的 $A$ 处遇险，发出求救信号．一艘救生船位于灯塔 $C$ 的南偏东 $40°$ 方向上，同时位于 $A$ 处的北偏东 $60°$ 方向上的 $B$ 处，救生船接到求救信号后，立即前往救援．求 $\mathit{AB}$ 的长（结果取整数）参考数据： $\tan 40°\approx 0.84$ ， $\sqrt{3}$ 取1.73．

如图，在河对岸有一棵大树 $A$，在河岸 $B$点测得 $A$在北偏东 $60°$方向上，向东前进 $120m$到达 $C$点，测得 $A$在北偏东 $30°$方向上，求河的宽度（精确到 $0.1m)$．参考数据： $\sqrt{2}\approx 1.414$， $\sqrt{3}\approx 1.732$．

如图，一艘轮船位于灯塔 $P$的北偏东 $60°$方向，与灯塔 $P$的距离为80海里的 $A$处，它沿正南方向航行一段时间后，到达位于灯塔 $P$的南偏东 $45°$方向的 $B$处，求此时轮船所在的 $B$处与灯塔 $P$的距离．（参考数据： $\sqrt{6}\approx 2.449$，结果保留整数）

随着中国经济的快速发展以及科技水平的飞速提高，中国高铁正迅速崛起．高铁大大缩短了时空距离，改变了人们的出行方式．如图， $A$， $B$两地被大山阻隔，由 $A$地到 $B$地需要绕行 $C$地，若打通穿山隧道，建成 $A$， $B$两地的直达高铁，可以缩短从 $A$地到 $B$地的路程．已知： $\angle \mathit{CAB}=30°$， $\angle \mathit{CBA}=45°$， $\mathit{AC}=640$公里，求隧道打通后与打通前相比，从 $A$地到 $B$地的路程将约缩短多少公里？（参考数据： $\sqrt{3}\approx 1.7$， $\sqrt{2}\approx 1.4)$

如图， $C$处是一钻井平台，位于东营港口 $A$的北偏东 $60°$方向上，与港口 $A$相距 $60\sqrt{2}$海里，一艘摩托艇从 $A$出发，自西向东航行至 $B$时，改变航向以每小时50海里的速度沿 $\mathit{BC}$方向行进，此时 $C$位于 $B$的北偏西 $45°$方向，则从 $B$到达 $C$需要多少小时？

南海是我国的南大门，如图所示，某天我国一艘海监执法船在南海海域正在进行常态化巡航，在A处测得北偏东30°方向上，距离为20海里的B处有一艘不明身份的船只正在向正东方向航行，便迅速沿北偏东75°的方向前往监视巡查，经过一段时间后，在C处成功拦截不明船只，问我海监执法船在前往监视巡查的过程中行驶了多少海里（最后结果保留整数）？

（参考数据： $\cos {75}^{\circ }=0.2588,\sin {75}^{\circ }=0.9659,\tan {75}^{\circ }=3.732,\sqrt{3}=1.732,\sqrt{2}=1.414$）

在某次海上军事学习期间，我军为确保△OBC海域内的安全，特派遣三艘军舰分别在O、B、C处监控△OBC海域，在雷达显示图上，军舰B在军舰O的正东方向80海里处，军舰C在军舰B的正北方向60海里处，三艘军舰上装载有相同的探测雷达，雷达的有效探测范围是半径为r的圆形区域．（只考虑在海平面上的探测）

（1）若三艘军舰要对△OBC海域进行无盲点监控，则雷达的有效探测半径r至少为多少海里？

（2）现有一艘敌舰A从东部接近△OBC海域，在某一时刻军舰B测得A位于北偏东60°方向上，同时军舰C测得A位于南偏东30°方向上，求此时敌舰A离△OBC海域的最短距离为多少海里？

（3）若敌舰A沿最短距离的路线以20海里/小时的速度靠近△OBC海域，我军军舰B沿北偏东15°的方向行进拦截，问B军舰速度至少为多少才能在此方向上拦截到敌舰A？

如图，我军的一艘军舰在南海海域巡航，在 $A$处时，某岛上的灯塔 $P$位于 $A$的南偏西 $30°$方向，距离为 $20\mathit{nmile}$，军舰沿南偏东 $15°$方向航行一段时间后到达 $B$处，此时，灯塔 $P$位于 $B$的西北方向上．

（1）分别求出 $\angle \mathit{PAB}$和 $\angle \mathit{PBA}$的大小；

（2）求 $B$到灯塔 $P$的距离．（结果保留1位小数，参考数据： $\sqrt{2}\approx 1.414$， $\sqrt{3}\approx 1.732)$

如图，线段 $\mathit{EF}$ 与 $\mathit{MN}$ 表示某一段河的两岸， $\mathit{EF}//\mathit{MN}$ ．综合实践课上，同学们需要在河岸 $\mathit{MN}$ 上测量这段河的宽度 $(\mathit{EF}$ 与 $\mathit{MN}$ 之间的距离），已知河对岸 $\mathit{EF}$ 上有建筑物 $C$ 、 $D$ ，且 $\mathit{CD}=60$ 米，同学们首先在河岸 $\mathit{MN}$ 上选取点 $A$ 处，用测角仪测得 $C$ 建筑物位于 $A$ 北偏东 $45°$ 方向，再沿河岸走20米到达 $B$ 处，测得 $D$ 建筑物位于 $B$ 北偏东 $55°$ 方向，请你根据所测数据求出该段河的宽度，（用非特殊角的三角函数或根式表示即可）

为了测量一条两岸平行的河流宽度，三个数学研究小组设计了不同的方案，他们在河南岸的点 $A$处测得河北岸的树 $H$恰好在 $A$的正北方向．测量方案与数据如下表：

课题	测量河流宽度
测量工具	测量角度的仪器，皮尺等
测量小组	第一小组	第二小组	第三小组
测量方案示意图
说明	点 $B$， $C$在点 $A$的正东方向	点 $B$， $D$在点 $A$的正东方向	点 $B$在点 $A$的正东方向，点 $C$在点 $A$的正西方向．
测量数据	$\mathit{BC}=60m$， $\angle \mathit{ABH}=70°$， $\angle \mathit{ACH}=35°$．	$\mathit{BD}=20m$， $\angle \mathit{ABH}=70°$， $\angle \mathit{BCD}=35°$．	$\mathit{BC}=101m$， $\angle \mathit{ABH}=70°$， $\angle \mathit{ACH}=35°$．

（1）哪个小组的数据无法计算出河宽？

（2）请选择其中一个方案及其数据求出河宽（精确到 $0.1m)$．（参考数据： $\sin 70°\approx 0.94$， $\sin 35°\approx 0.57$， $\tan 70°\approx 2.75$， $\tan 35°\approx 0.70)$

如图所示，在某海域，一艘指挥船在 $C$处收到渔船在 $B$处发出的求救信号，经确定，遇险抛锚的渔船所在的 $B$处位于 $C$处的南偏西 $45°$方向上，且 $\mathit{BC}=60$海里；指挥船搜索发现，在 $C$处的南偏西 $60°$方向上有一艘海监船 $A$，恰好位于 $B$处的正西方向．于是命令海监船 $A$前往搜救，已知海监船 $A$的航行速度为30海里 $/$小时，问渔船在 $B$处需要等待多长时间才能得到海监船 $A$的救援？（参考数据： $\sqrt{2}\approx 1.41$， $\sqrt{3}\approx 1.73$， $\sqrt{6}\approx 2.45$，结果精确到0.1小时）