初中数学解直角三角形的应用-方向角问题解答题

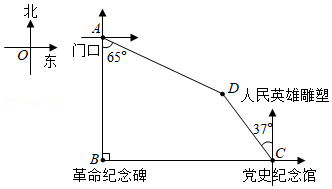
时代中学组织学生进行红色研学活动．学生到达爱国主义教育基地后，先从基地门口 $A$ 处向正南方向走300米到达革命纪念碑 $B$ 处，再从 $B$ 处向正东方向走到党史纪念馆 $C$ 处，然后从 $C$ 处向北偏西 $37°$ 方向走200米到达人民英雄雕塑 $D$ 处，最后从 $D$ 处回到 $A$ 处．已知人民英雄雕塑在基地门口的南偏东 $65°$ 方向，求革命纪念碑与党史纪念馆之间的距离（精确到1米）．（参考数据： $\sin 37°\approx 0.60$ ， $\cos 37°\approx 0.80$ ， $\tan 37°\approx 0.75$ ， $\sin 65°\approx 0.91$ ， $\cos 65°\approx 0.42$ ， $\tan 65°\approx 2.14)$

某天，北海舰队在中国南海例行训练，位于 $A$ 处的济南舰突然发现北偏西 $30°$ 方向上的 $C$ 处有一可疑舰艇，济南舰马上通知位于正东方向200海里 $B$ 处的西安舰，西安舰测得 $C$ 处位于其北偏西 $60°$ 方向上，请问此时两舰距 $C$ 处的距离分别是多少？

为了计算湖中小岛上凉亭 $P$到岸边公路 $l$的距离，某数学兴趣小组在公路 $l$上的点 $A$处，测得凉亭 $P$在北偏东 $60°$的方向上；从 $A$处向正东方向行走200米，到达公路 $l$上的点 $B$处，再次测得凉亭 $P$在北偏东 $45°$的方向上，如图所示．求凉亭 $P$到公路 $l$的距离．（结果保留整数，参考数据： $\sqrt{2}\approx 1.414$， $\sqrt{3}\approx 1.732)$

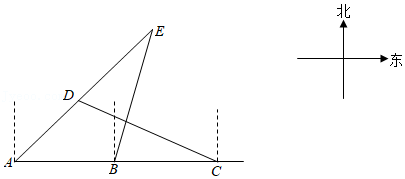
小张早起在一条东西走向的笔直马路上晨跑，他在 $A$ 处时， $D$ 处学校和 $E$ 处图书馆都在他的东北方向，当小张沿正东方向跑了 $600m$ 到达 $B$ 处时， $E$ 处图书馆在他的北偏东 $15°$ 方向，然后他由 $B$ 处继续向正东方向跑 $600m$ 到达 $C$ 处，此时 $D$ 处学校在他的北偏西 $63.4°$ 方向，求 $D$ 处学校和 $E$ 处图书馆之间的距离．（结果保留整数）

（参考数据： $\sin 63.4°\approx 0.9$ ， $\cos 63.4°\approx 0.4$ ， $\tan 63.4°\approx 2.0$ ， $\sqrt{2}\approx 1.4$ ， $\sqrt{3}\approx 1.7$ ， $\sqrt{6}\approx 2.4)$

如图，一段河流自西向东，河岸笔直，且两岸平行．为测量其宽度，小明在南岸边 $B$ 处测得对岸边 $A$ 处一棵大树位于北偏东 $60°$ 方向，他以 $1.5m/s$ 的速度沿着河岸向东步行 $40s$ 后到达 $C$ 处，此时测得大树位于北偏东 $45°$ 方向，试计算此段河面的宽度（结果取整数，参考数据： $\sqrt{3}\approx 1.732)$

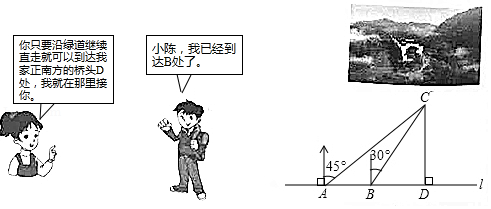
“五 $·$一”期间，小明到小陈家所在的美丽乡村游玩，在村头 $A$处小明接到小陈发来的定位，发现小陈家 $C$在自己的北偏东 $45°$方向，于是沿河边笔直的绿道 $l$步行200米到达 $B$处，这时定位显示小陈家 $C$在自己的北偏东 $30°$方向，如图所示．根据以上信息和下面的对话，请你帮小明算一算他还需沿绿道继续直走多少米才能到达桥头 $D$处（精确到1米）（备用数据： $\sqrt{2}\approx 1.414$， $\sqrt{3}\approx 1.732)$

小明周末与父母一起到遂宁湿地公园进行数学实践活动，在 $A$处看到 $B$、 $C$处各有一棵被湖水隔开的银杏树，他在 $A$处测得 $B$在北偏西 $45°$方向， $C$在北偏东 $30°$方向，他从 $A$处走了20米到达 $B$处，又在 $B$处测得 $C$在北偏东 $60°$方向．

（1）求 $\angle C$的度数；

（2）求两颗银杏树 $B$、 $C$之间的距离（结果保留根号）．

如图1，滑动调节式遮阳伞的立柱 $\mathit{AC}$垂直于地面 $\mathit{AB}$， $P$为立柱上的滑动调节点，伞体的截面示意图为 $\mathit{\Delta PDE}$， $F$为 $\mathit{PD}$的中点， $\mathit{AC}=2.8m$， $\mathit{PD}=2m$， $\mathit{CF}=1m$， $\angle \mathit{DPE}=20°$，当点 $P$位于初始位置 $P_0$时，点 $D$与 $C$重合（图 $2)$．根据生活经验，当太阳光线与 $\mathit{PE}$垂直时，遮阳效果最佳．

（1）上午 $10:00$时，太阳光线与地面的夹角为 $65°$（图 $3)$，为使遮阳效果最佳，点 $P$需从 $P_0$上调多少距离？（结果精确到 $0.1m)$

（2）中午 $12:00$时，太阳光线与地面垂直（图 $4)$，为使遮阳效果最佳，点 $P$在（1）的基础上还需上调多少距离？（结果精确到 $0.1m)$（参考数据： $\sin 70°\approx 0.94$， $\cos 70°\approx 0.34$， $\tan 70°\approx 2.75$， $\sqrt{2}\approx 1.41$， $\sqrt{3}\approx 1.73)$

如图， $A$， $B$是海面上位于东西方向的两个观测点，有一艘海轮在 $C$点处遇险发出求救信号，此时测得 $C$点位于观测点 $A$的北偏东 $45°$方向上，同时位于观测点 $B$的北偏西 $60°$方向上，且测得 $C$点与观测点 $A$的距离为 $25\sqrt{2}$海里．

（1）求观测点 $B$与 $C$点之间的距离；

（2）有一艘救援船位于观测点 $B$的正南方向且与观测点 $B$相距30海里的 $D$点处，在接到海轮的求救信号后立即前往营救，其航行速度为42海里 $/$小时，求救援船到达 $C$点需要的最少时间．

如图，一艘货船在灯塔 $C$ 的正南方向，距离灯塔257海里的 $A$ 处遇险，发出求救信号．一艘救生船位于灯塔 $C$ 的南偏东 $40°$ 方向上，同时位于 $A$ 处的北偏东 $60°$ 方向上的 $B$ 处，救生船接到求救信号后，立即前往救援．求 $\mathit{AB}$ 的长（结果取整数）参考数据： $\tan 40°\approx 0.84$ ， $\sqrt{3}$ 取1.73．

知识改变世界，科技改变生活．导航装备的不断更新极大方便了人们的出行．如图，某校组织学生乘车到黑龙滩（用 $C$表示）开展社会实践活动，车到达 $A$地后，发现 $C$地恰好在 $A$地的正北方向，且距离 $A$地13千米，导航显示车辆应沿北偏东 $60°$方向行驶至 $B$地，再沿北偏西 $37°$方向行驶一段距离才能到达 $C$地，求 $B$、 $C$两地的距离．（参考数据： $\sin 53°\approx \frac{4}{5}$， $\cos 53°\approx \frac{3}{5}$， $\tan 53°\approx \frac{4}{3})$

如图1，某社会实践活动小组实地测量两岸互相平行的一段河的宽度，在河的南岸边点 $A$处，测得河的北岸边点 $B$在其北偏东 $45°$方向，然后向西走 $60m$到达 $C$点，测得点 $B$在点 $C$的北偏东 $60°$方向，如图2．

（1）求 $\angle \mathit{CBA}$的度数．

（2）求出这段河的宽（结果精确到 $1m$，备用数据 $\sqrt{2}\approx 1.41$， $\sqrt{3}\approx 1.73)$．

如图，线段 $\mathit{EF}$ 与 $\mathit{MN}$ 表示某一段河的两岸， $\mathit{EF}//\mathit{MN}$ ．综合实践课上，同学们需要在河岸 $\mathit{MN}$ 上测量这段河的宽度 $(\mathit{EF}$ 与 $\mathit{MN}$ 之间的距离），已知河对岸 $\mathit{EF}$ 上有建筑物 $C$ 、 $D$ ，且 $\mathit{CD}=60$ 米，同学们首先在河岸 $\mathit{MN}$ 上选取点 $A$ 处，用测角仪测得 $C$ 建筑物位于 $A$ 北偏东 $45°$ 方向，再沿河岸走20米到达 $B$ 处，测得 $D$ 建筑物位于 $B$ 北偏东 $55°$ 方向，请你根据所测数据求出该段河的宽度，（用非特殊角的三角函数或根式表示即可）

如图， $C$处是一钻井平台，位于东营港口 $A$的北偏东 $60°$方向上，与港口 $A$相距 $60\sqrt{2}$海里，一艘摩托艇从 $A$出发，自西向东航行至 $B$时，改变航向以每小时50海里的速度沿 $\mathit{BC}$方向行进，此时 $C$位于 $B$的北偏西 $45°$方向，则从 $B$到达 $C$需要多少小时？

为了测量一条两岸平行的河流宽度，三个数学研究小组设计了不同的方案，他们在河南岸的点 $A$处测得河北岸的树 $H$恰好在 $A$的正北方向．测量方案与数据如下表：

课题	测量河流宽度
测量工具	测量角度的仪器，皮尺等
测量小组	第一小组	第二小组	第三小组
测量方案示意图
说明	点 $B$， $C$在点 $A$的正东方向	点 $B$， $D$在点 $A$的正东方向	点 $B$在点 $A$的正东方向，点 $C$在点 $A$的正西方向．
测量数据	$\mathit{BC}=60m$， $\angle \mathit{ABH}=70°$， $\angle \mathit{ACH}=35°$．	$\mathit{BD}=20m$， $\angle \mathit{ABH}=70°$， $\angle \mathit{BCD}=35°$．	$\mathit{BC}=101m$， $\angle \mathit{ABH}=70°$， $\angle \mathit{ACH}=35°$．

（1）哪个小组的数据无法计算出河宽？

（2）请选择其中一个方案及其数据求出河宽（精确到 $0.1m)$．（参考数据： $\sin 70°\approx 0.94$， $\sin 35°\approx 0.57$， $\tan 70°\approx 2.75$， $\tan 35°\approx 0.70)$