初中数学利用频率估计概率选择题

用频率估计概率，可以发现，抛掷硬币，“正面朝上”的概率为0.5，是指（ ）

A．连续掷2次，结果一定是“正面朝上”和“反面朝上”各1次

B．连续抛掷100次，结果一定是“正面朝上”和“反面朝上”各50次

C．抛掷2n次硬币，恰好有n次“正面朝上”

D．抛掷n次，当n越来越大时，正面朝上的频率会越来越稳定于0.5

某射击运动员在同一条件下的射击成绩记录如下：

射击次数	20	80	100	200	400	1000
"射中九环以上"的次数	18	68	82	168	327	823
"射中九环以上"的频率（结果保留两位小数）	0.90	0.85	0.82	0.84	0.82	0.82

根据频率的稳定性，估计这名运动员射击一次时"射中九环以上"的概率约是 $($ 　　 $)$

A．

0.90

B．

0.82

C．

0.85

D．

0.84

同时抛掷两枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，下列事件中是不可能事件的是（    ）

A．点数之和为12

B．点数之和小于3

C．点数之和大于4且小于8

D．点数之和为13

甲、乙两名同学在一次用频率去估计概率的实验中，统一了某一结果出现的频率绘出的统计图 如图所示，则符合这一结果的实验可能是（  ）

A．从一个装有2个白球和1个红球的袋子中任取两球，取到两个白球的概率

B．任意写一个正整数，它能被 2 整除的概率

C．抛一枚硬币，连续两次出现正面的概率

D．掷一枚正六面体的骰子，出现 1 点的概率

如图，正方形ABCD内接于⊙O，⊙O的直径为分米，若在这个圆面上随意抛一粒豆子，则豆子落在正方形ABCD内的概率是（ ）．

A．

B．

C．

D．

有一箱子装有3张分别标示4、5、6的号码牌，已知小武以每次取一张且取后不放回的方式，先后取出2张牌，组成一个二位数，取出第1张牌的号码为十位数，第2张牌的号码为个位数，若先后取出2张牌组成二位数的每一种结果发生的机会都相同，则组成的二位数为6的倍数的机率为何？（  ）

A．

B．

C．

D．

一枚质地均匀的正方体骰子，其六个面上分别刻有1、2、3、4、5、6六个数字，投掷这个骰子一次，则向上一面的数字小于3的概率是（  ）

A．

B．

C．

D．

从1、2、3、4、5、6中任取1个数，不大于4的概率是（ ）

A．

B．

C．

D．

某十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒，当你抬头看信号灯时，是黄灯的概率为（ ）

A．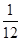

B．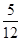

C．

D．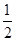

已知一个布袋里装有5个红球，3个白球，这些球除颜色外其余都相同．从该布袋里任意摸出1个球，若第一次是1个白球不放回，则第二次摸出白球的概率（     ）．

A．

B．

C．

D．

春节前夕，刘丽的奶奶为孩子们准备了一些红包，这些红包的外观相同，已知1个装的是100元，3个装的是50元，剩下的装的是20元．若刘丽从中随机拿出一个，里面装的是20元的红包的概率是，则装有20元红包的个数是（ ）

A．4

B．5

C．16

D．20

下列说法中不正确的是（ ）

A．“某射击运动员射击一次，正中把靶心”属于随机事件

B．“13名同学至少有两名同学的出生月份相同”属于必然事件

C．“在标准大气压下，当温度降到-1℃时，水结成冰”属于随机事件

D．“某袋中只有5个球，且都是黄球，任意摸出一球是白球”属于不可能事件

小明、小颖、和小凡都想去看山西第二届文博会，但现在只有一张门票，三人决定一起做游戏，谁获胜谁就去．游戏规则是：连续掷两枚质地均匀的硬币，若两枚正面朝上，则小明获胜；若两枚反面朝上，则小颖获胜；若一枚正面朝上，一枚反面朝上，则小凡获胜．关于这个游戏，下列判断正确的是（   ）

A．三个人获胜的概率相同

B．小明获胜的概率大

C．小颖获胜的概率大

D．小凡获胜的概率大

一个不透明的口袋里装有除颜色外都相同的5个白球和若干个红球，在不允许将球倒出来数的前提下，小亮为了估计其中的红球数，采用如下方法：先将口袋中的球摇匀，再从口袋里随机摸出一球，记下颜色，然后把它放回口袋中，不断重复上述过程，小亮共摸了100次，其中有10次摸到白球．因此小亮估计口袋中的红球大约有（ ）个．

A．45

B．48

C．50

D．55

在一个不透明的口袋中，装有5个红球3个白球，它们除颜色外都相同，从中任意摸出一个球，摸到红球的概率为（  ）

A．

B．

C．

D．