东营市为进一步加强和改进学校体育工作,切实提高学生体质健康水平,决定推进“一校一球队、一级一专项、一人一技能”活动计划.某校决定对学生感兴趣的球类项目(A:足球, B:篮球, C:排球,D:羽毛球,E:乒乓球)进行问卷调查,学生可根据自己的喜好选修一门,李老师对某班全班同学的选课情况进行统计后,制成了两幅不完整的统计图(如图).
(1)求出该班学生人数;
(2)将统计图补充完整;
(3)若该校共有学生3500名,请估计有多少人选修足球?
(4)该班班委5人中,1人选修篮球,3人选修足球,1人选修排球,李老师要从这5人中任选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.
九(1)班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会.抽奖方案如下:将一副扑克牌中点数为“2”、“3”、“3”、“5”、“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖.记每次抽出两张牌点数之差为x,按下表要求确定奖项.
| 奖项 |
一等奖 |
二等奖 |
三等奖 |
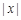 |
 |
 |
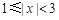 |
(1)用列表或画树状图的方法求出甲同学获一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
(本小题满分8分)小明和小丽用形状大小相同、面值不同的5张邮票设计了一个游戏,将面值1元、2元、3元的邮票各一张装入一个信封,面值4元、5元的邮票各一张装入另一个信封.游戏规定:分别从两个信封中各抽取1张邮票,若它们的面值和是偶数,则小明赢;若它们的面值和是奇数,则小丽赢.请你判断这个游戏是否公平,并说明理由.
在一个木箱中装有卡片共50张,这些卡片共有三种,它们分别标有1、2、3的字样,除此之外其他都相同,其中标有数字2卡片的张数是标有数字3卡片的张数的3倍少8张.已知从箱子中随机摸出一张标有数字1卡片的概率是 .
.
(1)求木箱中装有标1的卡片张数;
(2)求从箱子中随机摸出一张标有数字3的卡片的概率.
在歌唱比赛中,一位歌手分别转动如下的两个转盘(每个转盘都被分成3等份)一次,根据指针指向的歌曲名演唱两首曲目.
(1)转动转盘①时,该转盘指针指向歌曲“3”的概率是 ;
(2)若允许该歌手替换他最不擅长的歌曲“3”,即指针指向歌曲“3”时,该歌手就选择自己最擅长的歌曲“1”, 请用树形图或列表法中的一种,求他演唱歌曲“1”和“4”的概率.
在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格:
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于 ,求m的值.
,求m的值.
在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
| 事件A |
必然事件 |
随机事件 |
| m的值 |
|
|
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个球是黑球的概率等于 ,求m的值.
,求m的值.
有甲、乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字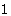 和
和 ;乙袋中有三个完全相同的小球,分别标有数字
;乙袋中有三个完全相同的小球,分别标有数字 、
、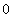 和
和 .小丽先从甲袋中随机取出一个小球,记下小球上的数字为
.小丽先从甲袋中随机取出一个小球,记下小球上的数字为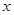 ;再从乙袋中随机取出一个小球,记录下小球上的数字为
;再从乙袋中随机取出一个小球,记录下小球上的数字为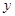 ,设点P的坐标为(
,设点P的坐标为(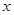 ,
,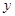 ).
).
(1)请用表格或树状图列出点P所有可能的坐标;
(2)求点P在一次函数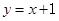 图像上的概率.
图像上的概率.
某人的钱包内有10元、20元和50元的纸币各1张,从中随机取出2张纸币.
(1)求取出纸币的总额是30元的概率;
(2)求取出纸币的总额可购买一件51元的商品的概率.
一只不透明袋子中装有1个红球、2个黄球,这些球除颜色外都相同。小明搅匀后从中意摸出一个球,记录颜色后放回、搅匀,再从中任意摸出1个球。用画树状图或列表法列出摸出球的所有等可能情况,并求两次摸出的球都是红球的概率。
有三张卡片(形状、大小、颜色、质地都相同),正面分别写上整式x2+1,-x2-2,3,将这三张卡片背面向上洗匀,从中任意抽取一张卡片,记卡片上的整式为A,再从剩下的卡片中任意抽取一张,记卡片上的整式为B,于是得到代数式 .
.
(1)请用画树状图或列表的方法,写出代数式 所有可能的结果;
所有可能的结果;
(2)求代数式 恰好是分式的概率.
恰好是分式的概率.
(本小题6分)为了参加中考体育测试,甲,乙,丙三位同学进行足球传球训练。球从一个人
脚下随机传到另一个人脚下,且每位传球人传球给其余两人的机会是均等的,由甲开始传球,共传三次。
(1)求请用树状图列举出三次传球的所有可能情况;
(2)传球三次后,球回到甲脚下的概率;
(3)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
(本小题满分8分)有两把不同的锁和四把不同的钥匙,其中两把钥匙恰好分别能打开这两把锁,其余的钥匙不能打开这两把锁.现在任意取出一把钥匙去开任意一把锁.请用列表或画树状图的方法求一次打开锁的概率.
某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面
调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要
求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题: 
(1)九(1)班的学生人数为 ,并把条形统计图补充完整;
(2)扇形统计图中m= ,n= ,表示“足球”的扇形的 圆心角是 度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
(本题8分)一个不透明的口袋中有四个完全相同的小球,它们分别标号为1,2,3,4
(1)随机摸取一个小球,直接写出“摸出的小球标号是3”的概率
(2)随机摸取一个小球然后放回,再随机摸出一个小球,直接写出下列结果:
① 两次取出的小球一个标号是1,另一个标号是2的概率
② 第一次取出标号是1的小球且第二次取出标号是2的小球的概率
试题篮
()