初中数学利用频率估计概率解答题

有一个不透明口袋，装有分别标有数字1，2，3，4的4个小球（小球除数字不同外，其余都相同），另有3张背面完全一样、正面分别写有数字1，2，3的卡片．小敏从口袋中任意摸出一个小球，小颖从这3张背面朝上的卡片中任意摸出一张，然后计算小球和卡片上的两个数的积．
（1）请你用列表或画树状图的方法，求摸出的这两个数的积为6的概率；
（2）小敏和小颖做游戏，她们约定：若这两个数的积为奇数，小敏赢；否则，小颖赢．你认为该游戏公平吗？为什么？如果不公平，请你修改游戏规则，使游戏公平．

小明和小芳做配紫色游戏，如图是两个可以自由转动的转盘，每个转盘被分成面积相等的几个扇形，并涂上图中所示的颜色．同时转动两个转盘，如果转盘A转出了红色，转盘B转出了蓝色，或者转盘A转出了蓝色，转盘B转出了红色，则红色和蓝色在一起配成紫色．
（1）利用列表或树状图的方法表示此游戏所有可能出现的结果；
（2）若出现紫色，则小明胜，否则小芳胜．此游戏的规则对小明、小芳公平吗？试说明理由．

某学习小组由3名男生和1名女生组成，在一次合作学习后，开始进行成果展示．
（1）如果随机抽取1名同学单独展示，那么女生展示的概率为               ．
（2）如果随机抽取2名同学共同展示，求同为男生的概率．

某大学举办教工男子篮球赛，由大学各个院系教工组成A、B、C、D、E五个代表队，由大学附属单位组成F、G、H三个代表队．通过抽签分组，比赛共分上下两个半区，上半区有A、D、E、G四个代表队，下半区有B、C、F、H四个代表队．若从上下半区各随机抽取一个代表队进行首场比赛，请列表或画树状图写出所有可能的结果，并计算首场比赛的两个代表队都是大学附属单位代表队的概率．

（本题8分）如图1，在一个不透明的袋子中装有四个球，分别标有字母A、B、C、D，这些球除了字母外完全相同，此外，有一面白色、另一面黑色、大小相同的四张正方形卡片，每张卡片两面的字母相同，分别标有字母A、B、C、D．最初，摆成如图2的样子，A．D是黑色，B．C是白色．

两次操作后观察卡片的颜色．
（如：第一次取出A、第二次取出B，此时卡片的颜色变成）
（1）求取四张卡片变成相同颜色的概率；
（2）求四张卡片变成两黑两白、并恰好形成各自颜色的矩形的概率．

（本题8分）一个不透明的布袋里装有2个白球，1个黑球和若干个红球，它们除颜色外其余都相同，从中任意摸出1个球，是白球的概率为．
（1）布袋里红球有多少个？
（2）先从布袋中摸出1个球后不放回，再摸出1个球，请用列表或画树状图等方法求出两次摸到的球都是白球的概率．

（本小题满分8分）甲口袋中装有3个相同的小球，它们分别写有数值﹣1，2，5；乙口袋中装有3个相同的小球，它们分别写有数值﹣4，2，3．现从甲口袋中随机取一球，记它上面的数值为x，再从乙口袋中随机取一球，记它上面的数值为y．设点A的坐标为（x，y）．
（1）请用树状图或列表法表示点A的坐标的各种可能情况；
（2）求点A落在的概率．

如图，A．B两个转盘分别被分成三个、四个相同的扇形，分别转动A盘、B盘各一次（若指针恰好指在分割线上，则重转一次，直到指针指向一个数字为止）．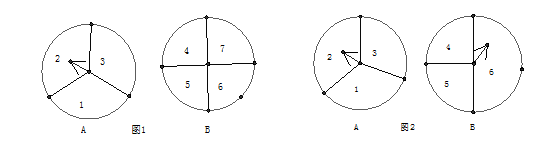

（1） 如图1，两个指针所指的区域内的数字之和大于7的概率为_________；
（2） 如果将图1中的转盘改为图2，其余不变，用列表或画树状图的方法，求两个指针所知区域的数字之和大于7 的概率．

（本小题8分）一只不透明的袋子里共有4个球，其中3个白球，1个红球，它们除颜色外均相同．
（1）从袋子中随机摸出一个球是白球的概率是多少？
（2）从袋子中随机摸出一个球，不放回袋子，摇匀袋子后再摸一个球，请用列表或画树状图的方法，求出两次摸出的球都是白球的概率．

（本小题8分）甲、乙两位同学玩转盘游戏，游戏规则：将圆盘平均分成三份，分别涂上红，黄，绿三种颜色，两位同学分别转动转盘两次（若压线，重新转）．若两次指针指到的颜色相同，则甲获胜；若两次指针指到的颜色是黄绿组合则乙获胜；其余情况则视为平局．

（1）请用画树状图的方法，列出所有可能出现的结果；
（2）试用概率说明游戏是否公平．

甲口袋中装有3个相同的小球，它们分别写有数值﹣1，2，5；乙口袋中装有3个相同的小球，它们分别写有数值﹣4，2，3．现从甲口袋中随机取一球，记它上面的数值为x，再从乙口袋中随机取一球，记它上面的数值为y．设点A的坐标为（x，y）．
（1）请用树状图或列表法表示点A的坐标的各种可能情况；
（2）求点A落在的概率．

小张同学报名参加校运动会，有下列5个项目可供选择：
径赛项目：100m，200m，800m （分别用A1、A2、 A3表示）；
田赛项目：立定跳远，跳高（分别用B1、B2表示）
（1）小张从5个项目中任选一个，恰好是径赛项目的概率为         ；
（2）小张从5个项目中任选两个，利用树状图或表格列举出所有可能的结果，并求恰好是一个田赛项目和一个径赛项目的概率

四张大小、质地均相同的卡片上分别标有1，2，3，4．现将标有数字的一面朝下扣在桌子上，然后由小明从中随机抽取一张（不放回），再从剩下的3张中随机取第二张
（1）用列表或画树状图的方法，列出小明前后两次取得的卡片上所标数字的所有可能情况；
（2）求取得的两张卡片上的数字之积为奇数的概率．

桌面上放有4张卡片，正面分别标有数字1，2，3，4．这些卡片除数字外完全相同，把这些卡片反面朝上洗匀后放在桌面上，甲从中任意抽出一张，记下卡片上的数字后仍反面朝上放回洗匀，乙也从中任意抽出一张，记下卡片上的数字，然后将这两数相加．
（1）请用列表或画树状图的方法求两数之和为5的概率；
（2）若甲与乙按上述方式做游戏，当两数之和为5时，甲胜；当两数之和不为5时，则乙胜．若甲胜一次得12分，谁先达到120分为胜．那么乙胜一次得多少分，这个游戏对双方公平？

袋中装有大小相同的2个红球和2个绿球．
（1）先从袋中摸出1个球后放回，混合均匀后再摸出1个球．求第一次摸到绿球，第二次摸到红球的概率；（用列表或数状图说明理由）
（2）先从袋中摸出1个球后不放回，再摸出1个球，则两次摸到的球中有1个绿球和1个红球的概率是多少？请直接写出结果．