初中数学利用频率估计概率解答题

小明想给小东打电话，但忘记了电话号码中的一位数字，只记得号码是284□9456（□表示忘记的数字）
⑴若小明从0至9的自然数中随机选取一个数字放在□位置，求他正确拨打小东电话的概率；
⑵若□位置的数字是不等式组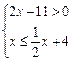的整数解，求□可能表示的数字．

一个不透明的口袋里装着红、黄、绿三种只有颜色不同的球，其中红球有2个，黄球有1个，从中任意摸出1球是红球的概率为.
（1）试求袋中绿球的个数；
（2）第1次从袋中任意摸出l球（不放回），第2次再任意摸出1球，请你用画树状图或列表格的方法，求两次都摸到红球的概率.

小明想给小东打电话，但忘记了电话号码中的一位数字，只记得号码是284□9456（□表示忘记的数字）
若小明从0至9的自然数中随机选取一个数字放在□位置，求他正确拨打小东电话的概率；
若□位置的数字是不等式组的整数解，求□可能表示的数字

小红和小慧玩纸牌游戏．如图是同一副扑克中的4张牌的正面，将它们正面朝下洗匀后放在桌上，小红先从中抽出一张，小慧从剩余的3张牌中也抽出一张．
请用树状图表示出两人抽牌可能出现的所有结果；
求抽出的两张牌都是偶数的概率．
 

一只不透明的袋子中装有4个质地、大小均相同的小球，这些小球分别标有3、4、5、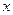，甲、乙两人每次同时从袋中各随机摸出1个小球，并计算摸出的这2个小球上数字之和，记录后都将小球放回袋中搅匀，进行重复实验，实验数据如下表：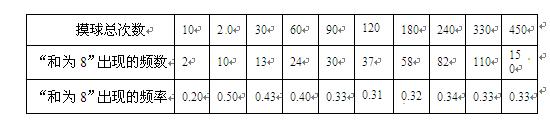

解答下列问题：
如果实验继续进行下去，根据上表数据，出现“和为8”的频率将稳定在它的概率附近，估计出现“和为8”的概率是          。
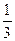如果摸出的这两个小球上数字之和为9的概率是，那么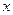的值可以取7吗？请用列表法或画树状图说明理由；如果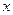的值不可以取7，请写出一个符合要求的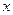值。

四张质地相同的卡片如图所示． 将卡片洗匀后，背面朝上放置在桌面上．
求随机抽取一张卡片，恰好得到数字2的概率；
小贝和小晶想用以上四张卡片做游戏，游戏规则见信息图．你认为这个游戏公平吗？请用列表法或画树状图法说明理由，若认为不公平，请你修改规则，使游戏变得公平．

小英和小丽用两个转盘做“配紫色”游戏，配成紫色小英得1分，否则小丽得1分，这个游戏对双方公平吗？（红色+蓝色=紫色，配成紫色者胜）
一个不透明的布袋里装有4个大小、质地均相同的乒乓球，每个球上面分别标有1、2、3、4，小林先从布袋中随机抽取一个乒乓球（不放回去），再从剩下的3个球中随机抽取第二个乒乓球。
请你列出所有可能的结果；

如图，有两个可以自由转动的均匀转盘A、B，转盘A被均匀地分成4等份，每份分别标上1、2、3、4四个数字；转盘B被均匀地分成6等份，每份分别标上1、2、3、4、5、6六个数字。有人为甲、乙两人设计了一个游戏，其规则如下：
　　⑴同时自由转动转盘A与B；
⑵转盘停止后，指针各指向一个数字（如果指针恰好指在分格线上，那么重转一次，直到指针停留在某一数字为止），用所指的两个数字作乘积，如果得到的积是偶数，那么甲胜；如果得到的积是奇数，那么乙胜（如转盘A指针指向3，转盘B指针指向5，3×5＝15，按规则乙胜）。你认为这样的规则是否公平？请说明理由；如果不公平，请你设计一个公平的规则，并说明理由。
　　

张慧同学给大家出了下面这样的问题，请你解答。
我的袋子里有3枚1角和1枚5角的硬币，如果我任意拿出两枚硬币，你知道前述之和大于5角的概率吗？
（要求：借助化树状图或列表的方法，列举所有等可能的结果，再进行计算。）

在一个口袋中有个完全相同的小球，把它们分别标号为，随机摸取一个小球然后放回，再随机地摸取一个小球。
（1）采用树状图法（或列表法）列出两次摸取小球出现的所有可能结果，并回答摸取两球出现的所以可能结果共有几种；
（2）求两次摸取的小球标号相同的概率；
（3）求两次摸取的小球标号的和等于的概率；
（4）求两次摸取的小球标号的和是的倍数或的倍数的概率。

“一方有难，八方支援”．四川汶川大地震牵动着全国人民的心，我市某医院准备从甲、乙、丙三位医生和A、B两名护士中选取一位医生和一名护士支援汶川．
若随机选一位医生和一名护士，用树状图（或列表法）表示所有可能出现的结果；
求恰好选中医生甲和护士A的概率．

在一个不透明的口袋中有分别标有数字﹣4，﹣1，2，5的四个质地、大小相同的小球，从口袋中随机摸出一个小球，记录其标有的数字作为x，不放回，再从中摸出第二个小球，记录其标有的数字为y．用这两个数字确定一个点的坐标为（x，y）．
（1）请用列表法或者画树状图法表示点的坐标的所有可能结果；
（2）求点（x，y）位于平面直角坐标系中的第三象限的概率．

如图，A、B、C、D四张卡片上分别写有，，，四个实数，从中任取两张卡片．

（1）请列举出所有可能的结果（用字母A，B，C，D表示）
（2）求取到的两个数都是无理数的概率。

某射击运动员在相同条件下的射击160次，其成绩记录如下：

射击次数	20	40	60	80	100	120	140	160
射中9环以上的次数	15	33		63	79	97	111	130
射中9环以上的频率	0.75	0.83	0.80	0.79	0.79		0.79	0.81

   （1）根据上表中的信息将两个空格的数据补全（射中9环以上的次数为整数，频率精确到0.01）；
（2）根据频率的稳定性，估计这名运动员射击一次时“射中9环以上”的概率（精确到0.1），
并简述理由.

（本小题满分4分）
甲口袋中装有2个小球，它们分别标有数字1、2，乙口袋中装有3个小球，它们分别标有数字3、4、5．现分别从甲、乙两个口袋中随机地各取出1个小球，请你用列举法（画树状图或列表的方法）求取出的两个小球上的数字之和为5的概率.