初中数学对称式和轮换对称式试题

如图，是一副学生用的三角板，在△ABC 中，∠C=90°， ∠A=60°，∠B=30°；在△中，∠C=90°， ∠A=45°，∠B=45°，且AB=" CB" ．若将边与边CA重合，其中点 与点C重合．将三角板绕点C（）按逆时针方向旋转，旋转过的角为，旋转过程中边与边AB的交点为M， 设AC=．

（1）计算的长；
（2）当=30°时，证明：∥AB；
（3）若=，当=45°时，计算两个三角板重叠部分图形的面积；
（4）当=60°时，用含的代数式表示两个三角板重叠部分图形的面积．
（参考数据：°= ，°= ，°= 
°=  ， °=  ， °=）

（本小题满分9分）如图，在平面直角坐标系中，四边形OABC为矩形，点A、B的坐标分别为（12，0）、（12，6），直线与y轴交于点P，与边OA交于点D，与边BC交于点E．

（1）若，求k的值；
（2）在（1）的条件下，当直线绕点P顺时针旋转时，与直线BC和x轴分别交于点N、M，问：是否存在NO平分∠CNM的情况？若存在，求线段DM的长；若不存在，请说明理由；
（3）在（1）的条件下，将矩形OABC沿DE折叠，若点O落在边BC上，求出该点坐标；若不在边BC上，求将（1）中的直线沿y轴怎样平移，使矩形OABC沿平移后的直线折叠，点O恰好落在边BC上．

如图2，边长为2的等边△ABC内接于⊙O，△ABC绕圆心O顺时针方向旋转得到△，A′C′分别与AB、AC交于E、D点，设旋转角度为．

（1）当＝     ，△A′B′C′与△ABC出现旋转过程中的第一次完全重合；
（2）当＝60°时（如图1），该图（     ）
A．是中心对称图形但不是轴对称图形   
B．是轴对称图形但不是中心对称图形
C．既是轴对称图形又是中心对称图形  
D．既不是轴对称图形也不是中心对称图形 
（3）如图2，当，△ADE的周长是否会发生变化，如会变化，说明理由，如不会变化，求出它的周长.

如图，在三角形纸片ABC中，∠BAC为锐角，AB=12cm，AC=15cm．按下列步骤折叠：第一次，把∠B折叠使点B落在AC边上，折痕为AD，交BC于点D；第二次折叠，使点A与点D重合，折痕分别交AB、AC于点E、F，EF与AD交于点O，展开后，连结DE、DF．

（1）试判断四边形AEDF的形状，并说明理由；
（2）求AF的长．

如图，直角坐标系中，Rt△DOC的直角边OC在轴上，∠OCD=90°，OD=6，OC=3，现将△DOC绕原点O按逆时针方向旋转，得到△AOB，且点A在轴上．

（1）请直接写出：∠A=       °；
（2）请求出线段OD扫过的面积．

在下图的网格中有一个三角形OAB，请你在网格中分别按下列要求画出图形

①画出向左平移3个单位后的三角形；
②画出绕点旋转180°后的三角形；
③画出沿y轴翻折后的图形．

本题满分11分．（为方便答题，可在答题卡上画出你认为必要的图形）
在Rt△ABC中，∠A=90°，AC=AB=4，D，E分别是边AB，AC的中点．若等腰Rt△ADE绕点A逆时针旋转，得到等腰RtRt△AD₁E₁，设旋转角为α（0＜α≤180°），记直线BD₁与CE₁的交点为P．
（1）如图1，当α=90°时，线段BD₁的长等于  ，线段CE₁的长等于  ；（直接填写结果）

（2）如图2，当α=135°时，求证：BD₁=CE₁ ，且BD₁⊥CE₁ ；

（3）求点P到AB所在直线的距离的最大值．（直接写出结果）

如图（1）将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍得△AB′C′ ，∠BAB′ ＝θ，，我们将这种变换记为[θ，n] ．如图（2），在△DEF中，∠DFE=90°，将 △DEF绕点D旋转，作变换[60°,n]得△DE′F′，如果点E、F、恰好在同一直线上，那么n=       ．

如图，在等边△ABC内有一点D，AD=5，BD=6，CD=4，将△ABD绕点A逆时针旋转，使AB与AC重合，点D旋转到点E，则∠CDE的正切值为             。

如图1，在Rt△ABC中，∠B=90°，BC=2AB=8，点D，E分别是边BC，AC的中点，连接DE. 将△EDC绕点C按顺时针方向旋转，记旋转角为α.
（1）问题发现
① 当时，；② 当时， 
（2）拓展探究
试判断：当0°≤α＜360°时，的大小有无变化？请仅就图2的情况给出证明.
（3）问题解决
当△EDC旋转至A、D、E三点共线时，直接写出线段BD的长.

在正方形ABCD中，BD是一条对角线.点P在射线CD上（与点C，D不重合），连接AP，平移△ADP，使点D移动到点C，得到△BCQ，过点Q作QH⊥BD于点H，连接AH、PH.

（1）若点P在线CD上，如图1，
①依题意补全图1；②判断AH与PH的数量关系与位置关系并加以证明；
（2）若点P在线CD的延长线上，且∠AHQ＝152°，正方形ABCD的边长为1，请写出求DP长的思路.（可以不写出计算结果）

平面上，矩形ABCD与直径为QP的半圆K如图摆放，分别延长DA和QP交于点O，且∠BOQ＝60°，OQ＝OD＝3，OP＝2，OA＝AB＝1．让线段OD及矩形ABCD位置固定，将线段OQ连带着半圆K一起绕着点O按逆时针方向形如旋转，设旋转角为α（0°≤α≤60°）．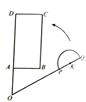

发现（1）当α＝0°，即初始位置时，点P____直线AB上．（填“在”或“不在”）求当α是多少时，OQ经过点B？
（2）在OQ旋转过程中．简要说明α是多少时，点P，A间的距离最小？并指出这个最小值：
（3）如图，当点P恰好落在BC边上时．求α及S_阴影．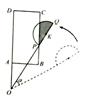

拓展如图．当线段OQ与CB边交于点M，与BA边交于点N时，设BM＝x（x＞0），用含x的代数式表示BN的长，并求x的取值范围．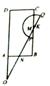

探究当半圆K与矩形ABCD的边相切时，求sin α的值．

如图，已知直线l∥l，一个45°角的顶点A在l上，过A作AD⊥l，垂足为D，AD＝6．将这个角绕顶点A旋转（角的两边足够长）．

（1）如下图，旋转过程中，若角的两边与l分别交于B、C，且AB＝AC，求BD的长．
为了解决这个问题，下面提供一种解题思路：如图，作∠DAP＝45°，AP与l相交于点P，过点C作CQ⊥AP于点Q．∵∠DAP＝∠BAC ＝45°，∴∠BAD＝∠CAQ， 请你接下去完成解答．
（2）旋转过程中，若角的两边与l分别交于E、F（E在F左面），且AE＞AF，DF＝ 2，求DE的长．请你借鉴（1）的做法在备用图中画图并解答这个问题．

规定：在平面直角坐标系xOy中，“把某一图形先沿x轴翻折，再沿y轴翻折”为一次变化．如图，已知正方形ABCD，顶点A（1，3），C（3，1）．若正方形ABCD经过一次上述变化，则点A变化后的坐标为       ，如此这样，对正方形ABCD连续做2015次这样的变化，则点D变化后的坐标为           ．

如图1，在Rt△ABC中，∠ACB=90°，E是边AC上任意一点（点E与点A，C不重合），以CE为一直角边作Rt△ECD，∠ECD=90°，连接BE，AD．
（1）若CA=CB，CE=CD
①猜想线段BE，AD之间的数量关系及所在直线的位置关系，直接写出结论；
②现将图1中的Rt△ECD绕着点C顺时针旋转锐角α，得到图2，请判断①中的结论是否仍然成立，若成立，请证明；若不成立，请说明理由；
（2）若CA=8,CB=6，CE=3，CD=4，Rt△ECD绕着点C顺时针转锐角α，如图3，连接BD，AE，计算的值．