初中数学对称式和轮换对称式试题

如图，菱形纸片ABCD中，∠A=60°，将纸片折叠，点A、D分别落在A′、D′处，且A′D′经过B，EF为折痕，当D′F⊥CD时，的值为    ．

（本小题满分9分）在锐角△ABC中，AB=4，BC=5，∠ACB=45°，将△ABC绕点B按逆时针方向旋转，得到△A₁BC₁．
（1）如图1，当点C₁在线段CA的延长线上时，求∠CC₁A₁的度数；
（2）如图2，连接AA₁，CC₁．若△ABA₁的面积为4，求△CBC₁的面积；
（3）如图3，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P₁，求线段EP₁长度的最大值与最小值．

如图1，已知△BAD和△BCE均为等腰直角三角形，∠BAD=∠BCE=90°，点M为DE的中点．过点E与AD平行的直线交射线AM于点N．
（1）当A，B，C三点在同一直线上时（如图1），求证：M为AN的中点；
（2）将图1中△BCE绕点B旋转，当A，B，E三点在同一直线上时（如图2），求证：△CAN为等腰直角三角形；
（3）将图1中△BCE绕点B旋转到图3的位置时，（2）中的结论是否仍然成立？若成立，试证明之；若不成立，请说明理由．

将一副三角尺（在Rt△ABC中，∠ACB=90°，∠B=60°；在Rt△DEF中，∠EDF=90°，∠E=45°）按如图①摆放，点D为AB的中点，DE交AC于点P，DF经过点C．

（1）求∠ADE的度数；
（2）将△DEF绕点D顺时针方向旋转角α（0°＜α＜60°），此时的等腰直角三角尺记为△DE′F′，DE′交AC于点M，DF′交BC于点N，如图②，试判断的值是否随着α的变化而变化？如果不变，请求出的值；如果变化，请说明理由．

在中，，，将一块等腰直角三角板的直角顶点放在斜边的中点处，将三角板绕点旋转，三角板的两直角边分别交、或其延长线于、两点，如图①与②是旋转三角板所得图形的两种情况．

（1）三角板绕点旋转，是否能成为等腰直角三角形？若能，指出所有情况（即给出是等腰直角三角形时的长），若不能，请说明理由；
（2）三角板绕点旋转，线段和之间有什么数量关系？用图①或②加以证明；
（3）若将三角板的直角顶点放在斜边上的点处（如图③），当时，和有怎样的数量关系？证明你发现的结论．

在正方形ABCD中，对角线AC与BD交于点O；在Rt△PMN中，∠MPN90°．
（1）如图1，若点P与点O重合且PM⊥AD、PN⊥AB，分别交AD、AB于点E、F，请直接写出PE与PF的数量关系；
（2）将图1中的Rt△PMN绕点O顺时针旋转角度α（0°<α<45°）．
①如图2，在旋转过程中（1）中的结论依然成立吗？若成立，请证明；若不成立，请说明理由；
②如图2，在旋转过程中，当∠DOM15°时，连接EF，若正方形的边长为2，请直接写出线段EF的长；
③如图3，旋转后，若Rt△PMN的顶点P在线段OB上移动（不与点O、B重合），当BD3BP时，猜想此时PE与PF的数量关系，并给出证明；当BDm·BP时，请直接写出PE与PF的数量关系．

已知直线m∥n，点C是直线m上一点，点D是直线n上一点，CD与直线m、n不垂直，点P为线段CD的中点．

（1）操作发现：直线l⊥m，l⊥n，垂足分别为A、B，当点A与点C重合时（如图①所示），连接PB，请直接写出线段PA与PB的数量关系： ．
（2）猜想证明：在图①的情况下，把直线l向上平移到如图②的位置，试问（1）中的PA与PB的关系式是否仍然成立？若成立，请证明；若不成立，请说明理由．
（3）延伸探究：在图②的情况下，把直线l绕点A旋转，使得∠APB=90°（如图③所示），若两平行线m、n之间的距离为2k．求证：PA•PB=k•AB．

（黄石）在△AOB中，C，D分别是OA，OB边上的点，将△OCD绕点O顺时针旋转到△OC′D′．

（1）如图1，若∠AOB=90°，OA=OB，C，D分别为OA，OB的中点，①AC′=BD′；②AC′⊥BD′；
（2）如图2，若△AOB为任意三角形且∠AOB=θ，CD∥AB，AC′与BD′交于点E，猜想∠AEB=θ是否成立？请说明理由．

如图1，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE、BF，交点为G．
可证：AE⊥BF；

（1）将△ABE绕点A逆时针方向旋转，使边AB正好落在AE上，得到△AHM，如图2，若AM和BF相交
于点N，当正方形ABCD的面积为4时，求四边形GHMN的面积．
（2）将△BCF沿BF对折，得到△BPF，如图3，延长FP交BA的延长线于点Q，求sin∠BQP的值；

（本小题7分）如图1，已知是等腰直角三角形，，点是的中点．作
正方形，使点、分别在和上，连接 ，．

（1）试猜想线段和的数量关系是          并证明．
（2）将正方形绕点逆时针方向旋转，判断（1）中的结论是否仍然成立？请利用图2证明你的结论；

（本小题6分）如右图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．将△ABC向左平移2格，再向上平移4格．

（1）请在图中画出平移后的△A′B′C′，
（2）再在图中画出△A′B′C′的高C′D′，并求出△ABC在整个平移过程中线段AC扫过的面积        

已知，正六边形ABCDEF在直角坐标系内的位置如图所示，A（﹣2，0），点B在原点，把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转，每次翻转60°，经过2015次翻转之后，点B的坐标是      ．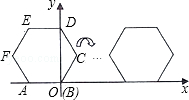

（本小题满分10分）如图1，△ABC是等腰直角三角形，四边形ADEF是正方形，D、F分别在AB、AC边上，此时BD=CF，BD⊥CF成立．
（1）当正方形ADEF绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF，BD⊥CF成立吗？若成立，请证明；若不成立，请说明理由．
（2）当正方形ADEF绕点A逆时针旋转45°时， AC与BG的交点为M， 当AB=4，AD=时，求线段CM的长．

如图，△ABC三个顶点坐标分别为，，，将△ABC绕点B顺时针旋转一定角度后使点A落在轴上，与此同时顶点C恰好落在的图像上， 则k的值为       ．

如图，四边形ABCD是矩形，AB＝6，BC＝8，点E在线段AD上，把△ABE沿直线BE翻折，点A落在点，的延长线交BC于点F，

（1）如图（1）求证FE＝FB；
（2）当点E在边AD上移动时，点的位置也随之变化，
①当点恰好落在线段BD上时，如图（2），求AE的长；
②在运动变化过程中，设，，求与的函数关系式，试判断能否平分矩形ABCD的面积，若能，求出的值，若不能，则说明理由；
（3）当点E在边AD上运动时，点D与点之间的距离也随之变化，请直接写出点D与点之间距离的变化范围．