初中数学对称式和轮换对称式试题

如图1，O为直线AB上一点，过点O作射线OC，∠AOC=30°，将一直角三角板（∠M=30°）的直角顶点放在点O处，一边ON在射线OA上，另一边OM与OC都在直线AB的上方．
（1）将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周．如图2，经过t秒后，OM恰好平分∠BOC．①求t的值；②此时ON是否平分∠AOC？请说明理由；
（2）在（1）问的基础上，若三角板在转动的同时，射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周，如图3，那么经过多长时间OC平分∠MON？请说明理由；
（3）在（2）问的基础上，经过多长时间OC平分∠MOB？请画图并说明理由．

画图计算：在8×8的方格纸中有△ABC 若A点的坐标（﹣2，0），C点的坐标（0，4）．
（1）在图中画出平面直角坐标系并写出B点的坐标．
（2）在图中画出△A′B′C′，使它与△ABC关于y轴对称，设小方格的边长为1，判断△A′B′C′的形状并求B′C′边上的高h的值．

如图，点P是∠AOB外的一点，点M，N分别是∠AOB两边上的点，点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在MN的延长线上．若PM=3cm，PN=4cm，MN=4.5cm，则线段QR的长为（ ）

A．4.5

B．5.5

C．6.5

D．7

如图，将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF，则四边形ABFD的周长为      ．

如图将如何变换才能够将下图所缺位置填满，形成两层阴影（ ）

A．顺时针旋转180度再向下平移

B．逆时针旋转180度再向下平移

C．顺时针旋转90度再向下平移

D．逆时针旋转90度再向下平移

如图，已知B（0，﹣4）射线BO绕B点逆时针旋转30°，交第二象限角平分线于P点，线段PB绕P点顺时针旋转45°交x轴于Q点，求BQ长．

已知等腰三角形一边长为4，一边的长为10，则等腰三角形的周长为（ ）

A．14

B．18

C．24

D．18或24

点A（—3，1）关于轴对称的点的坐标是      ．

在△ABC中，AB=AC，∠A=60°，点D是线段BC的中点，∠EDF=120°，DE与线段AB相交于点E，DF与线段AC（或AC的延长线）相交于点F．

（1）如图1，若DF⊥AC，垂足为F，AB=4，求BE的长；
（2）如图2，将（1）中的∠EDF绕点D顺时针旋转一定的角度，DF仍与线段AC相交于点F．求证：BE+CF=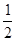AB；
（3）如图3，将（2）中的∠EDF继续绕点D顺时针旋转一定的角度，使DF与线段AC的延长线交与点F，作DN⊥AC于点N，若DN=FN，求证：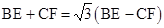

在直角三角形ABC中，∠BAC=90°，AB=AC,D为BC上一点，AB=BD,DE垂直于BC,交AC于E点，则图中等腰三角形个数是（  ）

A．3个

B．4个

C．5个

D．6个

如图，按要求涂阴影：

（1）将图形①平移到图形②；
（2）将图形②沿图中虚线翻折到图形③；
（3）将图形③绕其右下方的顶点旋转180°得到图形④．

如图，在边长为1的小正方形组成的网格中，A、B两点均在格点上，且坐标分别为A（3，2）；B（1，3）．

（1）点B关于y轴对称的点的坐标为      ．
（2）在网格线中描出点A、B，并画出△AOB，若将△AOB向左平移3个单位，再向上平移2个单位得到△A₁O₁B₁，则点A₁点坐标为      ．
（3）若以O、A、B、D为平行四边形的四个顶点，请写出第4个点D的坐标．

已知等腰△ABC的两边长分别为2和4，则等腰△ABC的周长为（ ）

A．8

B．10

C．8或10

D．12

在平面直角坐标系中，△ABC的三个顶点位置如图所示．

（1）请画出△ABC关于y轴对称的△A′B′C′（其中A′，B′，C′分别是A，B，C的对应点）；
（2）直接写出△A′B′C′三点的坐标：A′_________，B′__________，C′_________．
（3）求A B′的长。

在平面直角坐标系中，A（1, 2），B（3, 1），C（－2, －1）．

（1）在图中作出△ABC关于y轴的对称△A₁B₁C₁．
（2）写出△ABC关于x轴对称△A₂B₂C₂的各顶点坐标．
A₂ ______________   B₂ ______________    C₂______________