如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).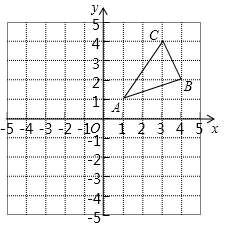
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
在如图的12×24的方格形纸中(每个小方格的边长都是1个单位)有一ΔABC.现先把ΔABC分别向右、向上平移8个单位和3个单位得到ΔA1B1C1;再以点O为旋转中心把ΔA1B1C1按顺时针方向旋转90º得到ΔA2B2C2.请在所给的方格形纸中作出ΔA1B1C1和ΔA2B2C2.

如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD.
如图,已知Rt△ABC中,∠C=90°.沿DE折叠,使点A与点B重合,折痕为DE.
(1)若DE=CE,求∠A的度数;
(2)若BC=6,AC=8,求CE的长.
如图,在平面直角坐标系中,A(-1,5),B(-3,1),C(-6,3).
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(2)写出△ABC关于x轴的对称图形△A2B2C2顶点A2、B2、C2的坐标.
如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.
(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.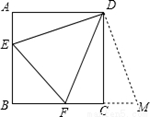
(1)求证:EF=FM;
(2)当AE=1时,求EF的长.21教育网
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,-1),B(-5,-4),C(-2,-3)
(1)作出△ABC向上平移6个单位,再向右平移7个单位的△A1B1C1。
(2)作出△ABC关于y轴对称的△A2B2C2,并写出点C2的坐标;
(3)将△ABC绕点O顺时针旋转900后得到△A3B3C3,请你画出旋转后的△A3B3C3
已知:如图,在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长.
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(1)作出格点△ 关于直线DE对称的△
关于直线DE对称的△ ;(2)作出△
;(2)作出△ 绕点
绕点 顺时针方向旋转
顺时针方向旋转 后的△
后的△ ;(3)△
;(3)△ 的周长为 ;(保留根号)
的周长为 ;(保留根号)

如图所示,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心O至少经过______次旋转而得到, 每一次旋转_______度.
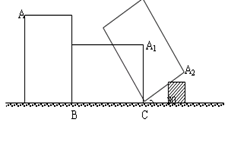
如图,小明使一长为4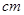 ,宽为3
,宽为3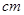 的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为
的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为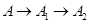 ,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
A.10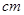 |
B.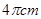 |
C.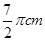 |
D.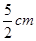 |
试题篮
()