初中数学对称式和轮换对称式试题

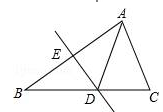
如图，将△ABC沿直线DE折叠后，使得点B与点A重合．已知AC=5cm，△ADC的周长为17cm，则BC的长为（ ）

A．7cm

B．10cm

C．12cm

D．22cm

在如图所示的直角坐标系中，每个小方格都是边长为1的正方形，△ABC的顶点均在格点上，点A的坐标是．

（1）将△ABC沿y轴正方向平移3个单位得到△，画出△，并写出点的坐标；
（2）画出△关于y轴对称的△，并写出点的坐标．

下面四个图形分别是节能、节水、绿色食品和低碳标志，在这四个标志中，是轴对称图形的是（   ）

A．

B．

C．

D．

如图，在Rt△ABC中，∠ACB=90°，点D、F分别在AB、AC上，CF=CB，连接CD，将线段CD绕点C按顺时针方向旋转90°后得CE，连接EF．

（1）请你探究∠CEF与∠ADC的数量关系，并证明你的结论；
（2）若EF∥CD，求∠BDC的度数．

如图，OE是∠AOB的平分线，BD⊥OA于点D，AC⊥BO于点C，则关于直线OE对称的三角形共有         对．

开车时，从后视镜中看到后面一辆汽车车牌号的后四位数是“”，则该车号牌的后四位应该是         ．

如图，点A关于y轴的对称点的坐标是                ．

探索与研究：
方法1：如图（a），对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得，所以∠BAE＝90°，且四边形ACFD是一个正方形，它的面积和四边形ABFE面积相等，而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和，根据图示写出证明勾股定理的过程；
方法2：如图（b），是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的，你能根据图示再写一种证明勾股定理的方法吗？

如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
（1）在图中画出与△ABC关于直线成轴对称的△A；
（2）线段被直线                        ；
（3）在直线上找一点P，使PB+PC的长最短，并算出这个最短长度．

如图，有a、b、c三户家用电路接入电表，相邻电路的电线等距排列，则三户所用电线（   ）

A．a户最长

B．b户最长

C．c户最长

D．三户一样长

如图，将Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置，D，D′分别是AB，A′B′的中点，且，已知AC=8cm，BC=6cm，求线段DD′的长．

一个图形无论经过平移还是旋转，有以下说法：
①对应线段平行；
②对应线段相等；
③对应角相等；
④图形的形状和大小都没有发生变化．
其中说法正确的是有          ．

如图，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2，△A′B′C可以由△ABC绕点C顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，连接AB′，且A、B′、A′在同一条直线上，则AA′的长为

A、6       B、4       C、3      D、2

如图是由三个小正方形组成的图形，请你在下面四幅图中各补画一个位置不同的小正方形，使补画后的图形为轴对称图形．（画出两个即可）

如图，△ABC的周长为30cm，把△ABC的边AC对折，使顶点C和A重合，折痕交BC边于点D，交AC边于点E，连接AD，若AE=4cm，则△ABD的周长是    

A．22cm

B．20cm

C．18cm

D．15cm