在边长为1的方格纸中建立直角坐标系,如图所示,O、A、B三点均为格点.
(1)直接写出线段OB的长;
(2)将△OAB绕点O沿逆时针方向旋转90°得到△OA′B′。请你画出△OA′B′,并求在旋转过程中,点B所经过的路径弧BB′的长度.
△ABC在平面直角坐标系xOy中的位置如图所示.
(1)作△ABC关于y轴成轴对称的△A1B1C1;
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2;则此三角形的面积为 .
(3)在x轴上求作一点P,使PA1+PC2的值最小,点P的坐标为 .
如图,△ABC三个定点坐标分别为A(﹣1,3),B(﹣1,1),C(﹣3,2).
(1)请画出△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2,请在第三象限内画出△A2B2C2,并求出S△A1B1C1:S△A2B2C2的值.
某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图(1)所示位置放置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.
如图,△ABC和△AED是等腰直角三角形,∠BAC=∠EAD=90°,点D、E在∠BAC的外部,连结DC,BE.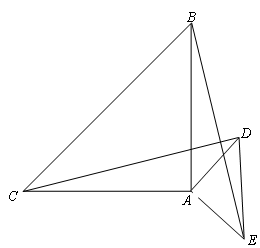
(1)求证:BE=CD;
(2)若将△AED绕点A旋转,直线CD交直线AB于点G,交直线BE于点K.
①如果AC=8,GA=2,求GC·KG的值;
②当△BED为等腰直角三角形时,请你直接写出AB∶BD的值.
在4×4的方格中有三个同样大小的正方形如图摆放,请你在图1—图3中的空白处添加一个正方形方格(涂黑),使它与其余三个正方形组成的新图形是一个轴对称图形.
如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3)
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(保留根号和π)
已知△ABC在平面直角坐标系中的位置如图所示.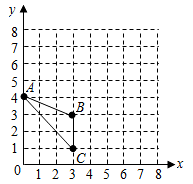
(1)分别写出图中点A和点C的坐标;
(2)画出△ABC绕点C按顺时针方向旋转90°后的△A′B′C′;
(3)求点A旋转到点A′所经过的路线长(结果保留π)
画图:在平面直角坐标系中, 的位置如图所示,且点A(-3,4),B(0,3)
的位置如图所示,且点A(-3,4),B(0,3)
|
 绕点O顺时针旋转90°后得到的
绕点O顺时针旋转90°后得到的 ;
;
 ,
, 的坐标;
的坐标;
(本题8分)在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABO的三个顶点都在格点上.
(1)以O为原点建立直角坐标系,点B的坐标为(-3,1),则点A的坐标为;
(2)画出△ABO绕点O顺时针旋转90°后的△OA1B1,并求线段OA扫过的面积.
如图,已知方格纸中有A、B、C三个格点,求作一个以A、B、C为顶点的格点四边形.
(1)在图1中作出的四边形是中心对称图形但不是轴对称图形.
(2)在图2中作出的四边形是轴对称图形但不是中心对称图形.
(3)在图3中作出的四边形既是轴对称图形又是中心对称图形.
试题篮
()