初中数学含绝对值的一元一次不等式试题

解不等式（组），并把解集在数轴上表示出来．
（1）
（2）．

某商店需要购进甲、乙两种商品共160件，其进价和售价如下表：

	甲	乙
进价（元/件）	15	35
售价（元/件）	20	45

（1）若商店计划销售完这批商品后能获利1100元，问甲、乙两种商品应分别购进多少件?
（2）若商店计划投入资金少于4300元，且销售完这批商品后获利多于1260元，请问有哪几种购货方案? 并直接写出其中获利最大的购货方案．

已知，，当          时，．

已知4x+y=3，且y≤7，则x的取值范围是        ．

对于实数m，n，定义一种运算“※”：m※n=m²﹣mn﹣3．下列说法错误的是（ ）

A．0※1=﹣3

B．方程x※2=0的根为x1=﹣1，x2=3

C．不等式组无解

D．函数y=x※（﹣2）的顶点坐标是（1，﹣4）

先阅读短文，然后回答短文后面所给出的问题：
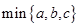对于三个数a、b、c的平均数，最小的数都可以给出符号来表示，我们规定 表示这三个数的平均数，表示这三个数中的最小的数，表示这三个数中最大的数．例如：，，；，．
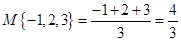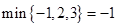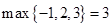（1）请填空：      ；若，则      ；
（2）若，求的取值范围；
（3）若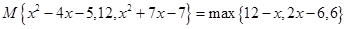，求的值．

不等式组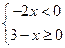的正整数解的个数是（  ）

A．1个

B．2个

C．3个

D．4个

. 如果不等式(a+1)x＞a+1的解集为x＜1，那么a的取值范围是. （ ）

A．a＞0

B．a＜0

C．a＞-1

D．a＜-1

如果不等式组有解,那么的取值范围是（  ）

A．>3

B．

C．<3

D．

不等式组的解集在数轴上表示正确的是（  ）

若不等式组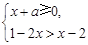有解，则a的取值范围是（  ）
A.a＞－1.    B.a≥－1.    C a≤1.    D.a＜1.

对x，y定义一种新运算T，规定：T（x，y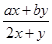）=（其中a、b均为非零常数），这里等式右边是通常的四则运算，例如：T（0，1）==b．
（1）已知T（1，-1）=-2，T（4，2）=1．
①求a，b的值；
②若关于m的不等式组恰好有3个整数解，求实数p的取值范围；
（2）若T（x，y）=T（y，x）对任意实数x，y都成立（这里T（x，y）和T（y，x）均有意义），则a，b应满足怎样的关系式？

一次函数y=kx+b的图像经过点（0，-4）且与正比例函数y=k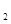x的图象交于点（2，-1）．
（1）分别求出这两个函数的表达式；
（2）求这两个函数的图象与x轴围成的三角形的面积；       
（3）直接写出不等式kx-4≥k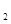x的解集。

对x，y定义一种新运算T，规定：T（x，y）=（其中a、b均为非零常数），这里等式右边是通常的四则运算，例如：T（0，1）==b．
（1）已知T（1，-1）=-2，T（4，2）=1．
①求a，b的值；
②若关于m的不等式组恰好有3个整数解，求实数p的取值范围；
（2）若T（x，y）=T（y，x）对任意实数x，y都成立（这里T（x，y）和T（y，x）均有意义），则a，b应满足怎样的关系式？

（本题10分）若不等式组的解集是，
（1）求代数式的值；
（2）若，，为某三角形的三边长，试求的值．