初中数学一元二次方程的最值解答题

随着人们环保意识的不断增强，我市家庭电动自行车的拥有量逐年增加．据统计，某小区2009年底拥有家庭电动自行车125辆，2011年底家庭电动自行车的拥有量达到180辆．
（1）若该小区2009年底到2012年底家庭电动自行车拥有量的年平均增长率相同，则该小区到2012年底电动自行车将达到多少辆？
（2）为了缓解停车矛盾，该小区决定投资3万元再建若干个停车位，据测算，建造费用分别为室内车位1000元/个，露天车位200元/个．考虑到实际因素，计划露天车位的数量不少于室内车位的2倍，但不超过室内车位的2.5倍，则该小区最多可建两种车位各多少个？试写出所有可能的方案．

先化简，再求值：（+）÷，其中x满足x²+x﹣2=0．

已知关于x的方程x²﹣2（k﹣1）x+k²=0有两个实数根x₁，x₂．
（1）求k的取值范围；
（2）若|x₁+x₂|=x₁x₂﹣1，求k的值．

已知关于x的方程（x﹣3）（x﹣2）﹣p²=0．
（1）求证：方程总有两个不相等的实数根．
（2）设方程的两根为x₁，x₂（x₁＜x₂），则当0≤p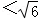时，请直接写出x₁和x₂的取值范围．

计算：
（1）用公式法解方程：x²+3x﹣2=0
（2）已知a²+a=0，请求出代数式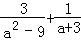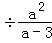（）的值．

已知函数y=kx+b的图象如图所示，则一元二次方程x²+x+k﹣1=0根的存在情况是（ ）

A．没有实数根

B．有两个相等的实数根

C．有两个不相等的实数根

D．无法确定

已知关于x的方程x²﹣（m+2）x+（2m﹣1）=0．
（1）求证：方程恒有两个不相等的实数根；
（2）若此方程的一个根是1，请求出方程的另一个根，并求以此两根为边长的直角三角形的周长．

某汽车4S店销售某种型号的汽车，每辆进货价为15万元，该店经过一段时间的市场调研发现：当销售价为25万元时，平均每周能售出8辆，而当销售价每降低0.5万元时，平均每周能多售出1辆．该4S店要想平均每周的销售利润为90万元，并且使成本尽可能的低，则每辆汽车的定价应为多少万元？

用适当的方法解下列方程
（1）2x²+x﹣1=0
（2）用配方法解方程：x²﹣4x+1=0．

现代互联网技术的广泛应用，催生了快递行业的高度发展，据调查，长沙市某家小型“大学生自主创业”的快递公司，今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件，现假定该公司每月投递的快递总件数的增长率相同．
（1）求该快递公司投递总件数的月平均增长率；
（2）如果平均每人每月最多可投递0.6万件，那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务？如果不能，请问至少需要增加几名业务员？

已知关于x的方程x²+（m+2）x+2m﹣1=0．
（1）求证：方程有两个不相等的实数根．
（2）若1是该方程的一个根．求m的值并求出此时方程的另一个根．

解方程：
（1）x²﹣8x﹣10=0；
（2）9t²﹣（t﹣1）²=0．

已知关于x的方程x²+2（k﹣3）x+k²=0有两个实数根x₁、x₂．
（1）求k的取值范围；
（2）若|x₁+x₂﹣9|=x₁x₂，求k的值．

（1）计算：2cos45°﹣（π+1）⁰
（2）解方程：x（2x﹣5）=4x﹣10．

某商场销售一批名牌衬衫，平均每天可售出20件，每件赢利40元，为了扩大销售，增加利润，尽量减少库存，商场决定采取适当的降价措施．经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件；
（1）若商场平均每天要赢利1200元，每件衬衫应降价多少元？
（2）每件衬衫降价多少元时，商场平均每天赢利最多？