二次函数y=2(x+3) 2-1的图象的顶点所在象限是().
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
已知二次函数y=ax2-bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②a-b+c<0;③b-2a<0;④abc>0,其中所有正确结论的序号是()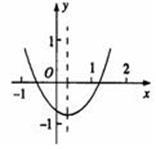
| A.①② | B.①②④ | C.①④ | D.②③④ |
把二次函数y=-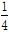 x2-x+3用配方法化成y=a(x-h)2+k的形式()
x2-x+3用配方法化成y=a(x-h)2+k的形式()
A.y=-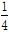 (x-2)2+2 (x-2)2+2 |
B.y=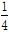 (x-2)2+4 (x-2)2+4 |
C.y=-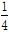 (x+2)2+4 (x+2)2+4 |
D.y=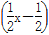 2+3 2+3 |
已知函数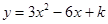 (
(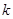 为常数)的图象经过点A(0.8,
为常数)的图象经过点A(0.8,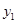 ),B(1.1,
),B(1.1,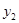 ),
),
C(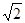 ,
,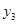 ),则有()
),则有()
A.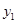 < <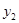 < <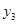 |
B.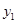 > >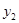 > >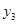 |
C.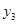 > >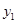 > >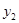 |
D.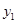 > >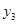 > >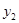 |
把抛物线 向下平移2个单位,再向右平移1个单位,所得到的抛物线是()
向下平移2个单位,再向右平移1个单位,所得到的抛物线是()
A. |
B.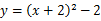 |
C.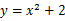 |
D. |
若抛物线y=ax2经过P(1,﹣2),则它也经过 ( )
| A.(2,1) | B.(﹣1,2) | C.(1,2) | D.(﹣1,﹣2) |
用配方法将二次函数y=3x2-4x-2写成形如y=a(x+m)2+n的形式,则m、n的值分别是()
A.m=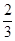 ,n= ,n=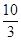 |
B.m=-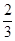 ,n=- ,n=-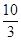 |
| C.m=2,n="6" | D.m=2,n=-2 |
抛物线y=﹣x2+bx+c的部分图象如图所示,要使y>0,则x的取值范围是()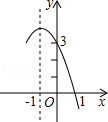
| A.﹣4<x<1 | B.﹣3<x<1 | C.x<﹣4或x>1 | D.x<﹣3或x>1 |
若点P1(﹣1,y1),P2(﹣2,y2),P3(1,y3),都在函数y=x2﹣2x+3的图象上,则()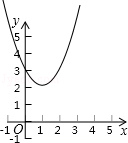
| A.y2<y1<y3 | B.y1<y2<y3 | C.y2>y1>y3 | D.y1>y2>y3 |
试题篮
()