如图是抛物线
的一部分，且其过点（3,0），对称轴为直线x=1，则下列结论正确的有_________
①abc＞0
②方程
有两个不相等的实数根
③a-b+c=0
④当x＞0时，y随x的增大而增大
⑤不等式
的解为x＞3
⑥3a+2c＜0
（本小题满分10分）如图，平面直角坐标系中，矩形OABC的顶点A（0，3），C（-1，0）．将矩形OABC绕原点顺时针旋转90°，得到矩形
．解答下列问题：
（1）求出直线
的函数解析式；
（2）直线与
轴交于点M、与y轴交于点N，抛物线
的图象经过点C、M、N，求抛物线的函数解析式；
（3）将△MON沿直线MN翻折，点O落在点P处，请你判断点P是否在抛物线上，说明理由．
（满分10分）如图，已知抛物线经过A（-2，0），B（-3，3）及原点O，顶点为C．
（1）求抛物线的解析式；
（2）若点D在抛物线上，点E在抛物线的对称轴上，且A、O、D、E为顶点的四边形是平行四边形，求点D的坐标；
（3）P是抛物线上的第一象限内的动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以P、M、A为顶点的三角形△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．
如图，抛物线经过A（﹣1，0），B（5，0），C（0，
）三点．
（1）求抛物线的解析式；
（2）在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标；
（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．
（本题10分）八一中学初三年级的一场篮球赛中，如图队员甲正在投篮，已知球出手时离地面高
m，与球圈中心的水平距离为7m，当球出手后水平距离为4m时到达最大高度4m．设篮球运行轨迹为抛物线，篮圈距地面3m．
（1）建立如图的平面直角坐标系，问此球能否准确投中？
（2）此时，若对方队员乙在甲前面1m处跳起盖帽拦截，已知乙的最大摸高为3．1m，那么他能否获得成功？
（本题10分）如图，二次函数y＝a
－4x＋c的图象过原点，与x轴交于点A（－4，0）．
（1）求二次函数的解析式；
（2）在抛物线上存在点P，满足S△AOP＝8，请求出点P的坐标．
（本题10分）如图，直线y＝x＋m和抛物线y＝
＋bx＋c都经过点A（1，0），
B（3，2）．
（1）求m的值和抛物线的解析式；
（2）求不等式x2＋bx＋c＞x＋m的解集．（直接写出答案）
（本题10分）已知二次函数
．
（1）用配方法把该函数化为
（其中a、h、k都是常数且a≠0）的形式，并指出函数图象的对称轴和顶点坐标；
（2）求这个函数图象与x轴、y轴的交点坐标．
（本题10分）如图，利用一面长为34米的墙，用铁栅栏围成一个矩形自行车场地ABCD，在AB和BC边各有一个2米宽的小门（不用铁栅栏）．设矩形ABCD的边AD长为x米，AB长为y米，矩形的面积为S平方米，且x＜y．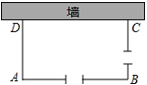
（1）若所用铁栅栏的长为40米，求y与x的函数关系式，并直接写出自变量x的取值范围；
（2）在（1）的条件下，求S与x的函数关系式，并求出怎样围才能使矩形场地的面积为192平方米？
已知一次函数y=ax+b的图象上有两点A、B，它们的横坐标分别是3，－1，若二次函数y=
x2的图象经过A、B两点．
（1）请求出一次函数的表达式；
（2）设二次函数的顶点为C，求△ABC的面积．
如图所示,点P是抛物线y=x2上第一象限内的一个点,点A（3,0）．
（1）令点P的坐标为（x,y）,求△OPA的面积S与y的关系式．
（2）S是y的什么函数?S是x的什么函数?
某公司推销一种产品，公司付给推销员的月报酬有两种方案如图所示：其中方案一所示图形是顶点B在原点的抛物线的一部分，方案二所示图形是射线．设推销员推销产品的数量为x（件），付给推销员的月报酬为y（元）．
（1）分别求两种方案中y关于x的函数关系式；
（2）当销售达到多少件时，两种方案月报酬差额将达到3800元？
（3）若公司决定改进“方案二”：保持基本工资不变，每件报酬增加m元，使得当销售员销售产量达到40件时，两种方案的报酬差额不超过1000元．求m的取值范围．
已知二次函数h=x2﹣（2m﹣1）x+m2﹣m（m是常数，且m≠0）
（1）证明：不论m取何值时，该二次函数图象总与x轴有两个交点；
（2）若A（n﹣3，n2+2）、B（﹣n+1，n2+2）是该二次函数图象上的两个不同点，求二次函数解析式和m的值；
（3）设二次函数h=x2﹣（2m﹣1）x+m2﹣m与x轴两个交点的横坐标分别为x1，x2（其中x1＞x2），若y是关于m的函数，且y=2﹣
，请结合函数的图象回答：当y＜m时，求m的取值范围．
试题篮
()
粤公网安备 44130202000953号
x2+bx+c的顶点为M，对称轴是直线x=1，与x轴的交点为A（﹣3，0）和B．将抛物线y=
