初中数学二次函数在给定区间上的最值解答题

某公司生产的某种商品每件成本为20元，经过市场调研发现，这种商品在未来40天内的日销售量m（件）与时间t（天）满足一次函数且关系如下表：

时间t（天）	1	3	6	10	36	…
日销售量m（件）	94	90	84	76	24	…

 
未来40天内，每天的销售价格y（元）与时间t（天）的函数关系式如下：

每天的销售价格y（元）	当1≤t≤20时，y1=t+25
当20＜t≤40时，y2=t+40

 
（1）求日销售量m（件）与时间t（天）的函数关系；
（2）请预测未来40天中哪一天的日销售利润最大，最大日销售利润是多少；
（3）在实际销售的前20天中，该公司决定每销售一件商品就捐赠a元（a＜4）给希望工程，公司通过销售记录发现，前20天中，每天扣除捐赠后的日销售利润随时间t（天）的增大而增大，求a的取值范围．

如图，抛物线y=－x²+bx+c与x轴交于A（－1,0）,B（5,0）两点，直线y=－x+3与y轴交于点C，，与x轴交于点D．点P是x轴上方的抛物线上一动点，过点P作PF⊥x轴于点F，交直线CD于点E．设点P的横坐标为m。

（1）求抛物线的解析式；
（2）若PE =5EF,求m的值；
（3）若点E^/是点E关于直线PC的对称点、是否存在点P，使点E^/落在y轴上？若存在，请直接写出相应的点P的坐标；若不存在，请说明理由。

今年，6月12日为端午节．在端午节前夕，三位同学到某超市调研一种进价为2元的粽子的销售情况．请根据小丽提供的信息，解答小华和小明提出的问题．

（1）小华的问题解答：
（2）小明的问题解答：

（14’）如图，在平面直角坐标系中，A、B为轴上两点，C、D为轴上的两点，经过点A、C、B的抛物线的一部分C₁与经过点A、D、B的抛物线的一部分C₂组合成一条封闭曲线，我们把这条封闭曲线称为“蛋线”．已知点C的坐标为（0，），点M是抛物线C₂：（＜0）的顶点．

（1）求A、B两点的坐标；
（2）“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；
（3）当△BDM为直角三角形时，求的值．

如图，在平面直角坐标系中，点A的坐标为（12，−8），点B、C在x轴上，tan∠ABC＝，AB＝AC，AH⊥BC于H，D为AC的中点，BD交AH于点M．

（1）求过B、C、D三点的抛物线的解析式，并求出抛物线顶点E的坐标；
（2）过点E且平行于AB的直线l交y轴于点G，若将（2）中的抛物线沿直线l平移，平移后的抛物线交y轴于点F，顶点为E′（点E′在y轴右侧）．是否存在这样的抛物线，使△E′FG为等腰三角形？若存在，请求出此时顶点E’的坐标；若不存在，请说明理由．

如图，边长为15cm的等边△ABC的顶点B、C都在直线l上，现将一块直角三角尺DEF按如图位置摆放，其中DE＝EF＝12cm，∠DEF＝90°，E、F在直线l上，且F与B重合．若将三角尺DEF沿直线l以3cm/s的速度向右移动，设运动时间为t（s）．
（1）请直接写出三角尺DEF的顶点D落在△ABC内部（不含边上）时，时间t的取值范围：______________；
（2）在运动过程中，设△DEF与△ABC的重叠部分面积为S（cm²），试求在点F到达点C之前，S与t的函数关系式，并写出自变量t的取值范围．

如图，有一座拱桥是抛物线形，它的跨度AB为60米，拱桥最高处点P到AB的距离为18米，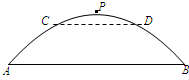

（1）建立恰当的坐标系，求出抛物线的解析式；
（2）当洪水泛滥，水面上升，若拱桥的水面跨度只有30米时，则必须马上采取紧急措施．现已知拱顶P离水面CD的距离只有4米，问：是否要采取紧急措施？并说明理由．

（本小题满分12分）已知抛物线经过点A（-3，0），B（1，0）和点C（0，-3）．
（1）求抛物线的解析式；
（2）如图，若抛物线的顶点为P，连接PC并延长与x轴相交于点M，x轴上另一点N，若，求点N的坐标；

（3）在上述条件下，在抛物线或坐标轴上是否存在点G，使△GMC与△OPC相似？若存在，求点G的坐标；若不存在，请说明理由．

如图，抛物线与x轴相交于点A（1，0）与点B ，与y轴相交于点C．

（1）确定抛物线的解析式；
（2）连接AC、BC，△AOC与△COB相似吗？并说明理由．
（3）点N在抛物线的对称轴上，在抛物线上是否存在点M，使得以点N、M、A、B为顶点的四边形是平行四边形？若存在，求出对应的点M、N的坐标；若不存在，请说明理由．

某商场出售一批进价为3元的小工艺品，在市场营销中发现此工艺品的日销售单价x（单位：元）与日销售量y（单位：个）之间有如下关系：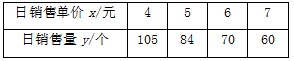

（1）根据表中数据反映规律试确定y与x之间的函数关系式；
（2）设经营此小工艺品的日销售利润为S元，求出S与x之间的函数关系式；
（3）物价局规定小商品的利润不得高于进价的200%，请你求出当日销售单价x定为多少时，才能获得最大日销售利润？最大日销售利润是多少？

如图，直线与轴、轴分别交于点A、B，抛物线经过点A、B．求：

（1）点A、B的坐标；
（2）抛物线的函数表达式；
（3）在抛物线对称轴上是否存在点P，使得以A、B、P为顶点的三角形为等腰三角形，若存在，求点P的坐标；若不存在，请说明理由．

如图，抛物线y=ax²+bx-4a经过A(-1，0)、C(0，4)两点，与x轴交于另一点B．

（1）求抛物线的解析式；
（2）已知点D(m，m+1)在第一象限的抛物线上，求点D关于直线BC对称的点的坐标；
（3）在（2）的条件下，连接BD，点P为抛物线上一点，且∠DBP=45°，求点P的坐标．

（本题10分）某工厂设门市部专卖某产品，该产品每件成本30元，从开业一段时间的每天销售统计中，随机抽取一部分情况如下表所示：

销售单位（元）	50	60	70	75	80	85	…
日销售量（件）	300	240	180	150	120	90	…

 
假设每天定的售价是不变的，且每天销售情况均服从这种规律．
（1）观察表格判断日销售量与销售价格之间的函数关系，并求出函数关系式；
（2）门市部原设定两名销售员，但当销售量较大时，在每天售出量超过198件时，则必须增派一名营业员才能保证营业有序进行．设营业员每人每天工资为40元，求每件产品应定价多少元，才能使每天门市部纯利润最大？（纯利润=总销售﹣成本﹣营业员工资）

（本小题8分）已知抛物线y=+bx+c过点（0，0），（1，3），求抛物线的解析式，并求出抛物线的顶点坐标．

（本题12分）如图，在平面直角坐标系中，已知OA＝2，OC＝4，⊙M与轴相切于点C，与轴交于A，B两点，∠ACD＝90°，抛物线经过A，B，C三点．

（1）求证：∠CAO＝∠CAD；
（2）求弦BD的长；
（3）在抛物线的对称轴上是否存在点P使ΔPBC是以BC为腰的等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．