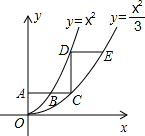
如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与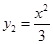 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则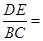 .
.
某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数表达式是y = 60x-1.5x2,该型号飞机着陆后需滑行 m才能停下来.
二次函数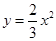 的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An﹣1BnAn=60°,菱形An﹣1BnAnCn的周长为.
的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An﹣1BnAn=60°,菱形An﹣1BnAnCn的周长为.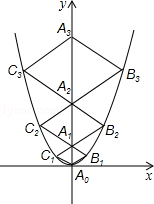
如图,在相距2米的两棵树间拴一根绳子做一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小芳距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为 米.
在平面直角坐标系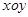 中,直线
中,直线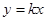 (
(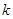 为常数)与抛物线
为常数)与抛物线 交于
交于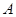 ,
,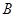 两点,且
两点,且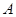 点在
点在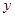 轴左侧,
轴左侧,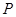 点的坐标为
点的坐标为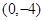 ,连接
,连接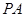 ,
,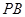 .有以下说法:①
.有以下说法:①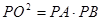 ;②当
;②当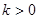 时,
时,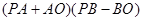 的值随
的值随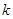 的增大而增大;③当
的增大而增大;③当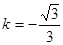 时,
时,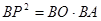 ;④
;④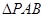 面积的最小值为
面积的最小值为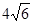 .其中正确的是_______________.(写出所有正确说法的序号)
.其中正确的是_______________.(写出所有正确说法的序号)
如图,在平面直角坐标系xOy中,已知抛物线(0≤x≤3)在x轴上方的部分,记作C1,它与x轴交于点O,A1,将C1绕点A1旋转180°得C2,C2与x 轴交于另一点A2.请继续操作并探究:将C2绕点A2旋转180°得C3,与x 轴交于另一点A3;将C3绕点A2旋转180°得C4,与x 轴交于另一点A4,这样依次得到x轴上的点A1,A2,A3,…,An,…,及抛物线C1,C2,…,Cn,….则点A4的坐标为;Cn的顶点坐标为(n为正整数,用含n的代数式表示) .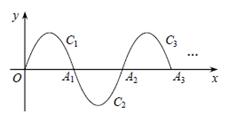
如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与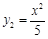 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 = .
= .
如图,二次函数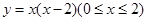 的图象,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……如此进行下去,直至得C14. 若P(27,m)在第14段图象C14上,则m=.
的图象,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……如此进行下去,直至得C14. 若P(27,m)在第14段图象C14上,则m=.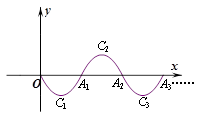
如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=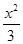 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则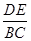 =.
=.
如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C2015.
若P(m,2),在第2015段抛物线C2015上,则m= 6043或6044 .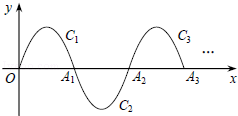
在直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若 ,则称点Q为点P的“可控变点”.
,则称点Q为点P的“可控变点”.
例如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).
(1)若点(﹣1,﹣2)是一次函数y=x+3图象上点M的“可控变点”,则点M的坐标为 ;(2)若点P在函数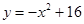 (
(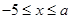 )的图象上,其“可控变点”Q的纵坐标y′的取值范围是
)的图象上,其“可控变点”Q的纵坐标y′的取值范围是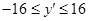 ,则实数a的取值范围是 .
,则实数a的取值范围是 .
如图,已知抛物线C1:y=a1x2+b1x+c1和C2:y=a2x2+b2x+c2都经过原点,顶点分别为A,B,与x轴的另一个交点分别为M、N,如果点A与点B,点M与点N都关于原点O成中心对称,则抛物线C1和C2为姐妹抛物线,请你写出一对姐妹抛物线C1和C2,使四边形ANBM恰好是矩形,你所写的一对抛物线解析式是_______________________和_________________________
试题篮
()