初中数学面积及等积变换选择题

如图，该几何体的主视图是

下列图形中是中心对称图形的是

按右边方格中的规律，在下面4个符号中选择一个填入方格左上方的空格内（   ）

将一张等边三角形纸片按图1－①所示的方式对折，再按图1－②所示的虚线剪去一个小三角形，将余下纸片展开得到的图案是 (       )

探索规律：根据下图中箭头指向的规律，从2004到2005再到2006，箭头的方向是（　　）

将图（1）所示的正六边形进行分割得到图（2），再将图（2）里的三个小正
六边形的其中之一按同样的方式进行分割得到图（3），接着再将图（3）中最小的三个正六边形的其中之一按同样的方式进行分割…，则第n 图形中共有（       ）个正六边形．

A．3n

B．3n-2

C．3n+2

D．3(n-2)

古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”，而把1、4、9、16 … 这样的数称为“正方形数”.从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中，符合这一规律的是（    ）

A．13 = 3+10

B．25 =" 9+16"

C．36 = 15+21

D．49 = 18+31

在下列图形中，沿着虚线将长方形剪成两部分，那么由这两部分既能拼成三角形又能拼成平行四边形和梯形的可能是        （      ）
                                                               

如图，把一个正方形经过上折、右折、下方折三次对折后沿虚线剪下，则所得图形是

如图所示，将向右平移3个单位长度后得再将绕点旋转后得到则下列说法正确的是     （   ）

A．的坐标为

B．

C．

D．

下列图案是用四种基本图形按照一定规律拼成的，第10个图案中的最下面一行从左至右的第2个基本图形应是（    ）

将一正方形纸片按图中（1）、（2）的方式依次对折后，再沿(3)中的虚线裁剪，最后将（4）中的纸片打开铺平，所得图案应该是下面图案中的             （    ） 

                                                              

如图，把其中的一个小正方形看作基本图形，这个图形中不含的变换是（   ）

A．相似（相似比不为1）

B．平移

C．对称

D．旋转

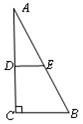
如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形；②等腰梯形；③有一个角为锐角的菱形；④正方形.那么以上图形一定能被拼成的个数为(      )

A．1

B．2

C．3

D．4

如图 将如何变换才能够将下图所缺位置填满，形成两层阴影（    ）

A．顺时针旋转180度再向下平移	B．逆时针旋转180度再向下平移
C．顺时针旋转90度再向下平移	D．逆时针旋转90度再向下平移