初中数学三角形的五心试题

如图已知四边形ABCD是⊙O的内接四边形，且AB=CD=5，AC=7，BE=3，下列命题：
①△AED∽△BEC
②∠AEB=90°
③∠BDA=45° 
④图中全等的三角形共有3对．
其中正确的命题有（    ）个．

A．1

B．2

C．3

D．4

如图，将△ABC沿AB方向平移得到△DEF，△ABC与△DEF重叠部分（图中阴影部分）的面积是△ABC的．已知BC=3，求△ABC平移的距离．

数学课上，李老师出示了如下框中的题目．

小敏与同桌小聪讨论后，进行了如下解答：
（1）特殊情况•探索结论
当点E为AB的中点时，如图1，确定线段AE与的DB大小关系．请你直接写出结论：AE__________DB（填“＞”，“＜”或“=”）．
（2）特例启发，解答题目
解：题目中，AE与DB的大小关系是：AE__________DB（填“＞”，“＜”或“=”）．理由如下：
如图2，过点E作EF∥BC，交AC于点F，（请你完成以下解答过程）
（3）拓展结论，设计新题
在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC．若△ABC的边长为1，AE=2，求CD的长．

如图，在等腰Rt△ABC中，AB=AC，CE是∠ACB的平分线，ED⊥BC，垂足为D．

（1）请写出图中所有的等腰三角形（不包括△ABC）；
（2）请判断AD与CE是否垂直，并说明理由；
（3）如果AB=2，求AC+AE的值．

如图，已知△ABC是等边三角形，D为边AC的中点，AE⊥EC，BD=EC．

（1）求证：△BDA≌△CEA；
（2）请判断△ADE是什么三角形，并说明理由．

如图，已知△ABC，其中AB=AC．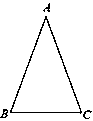

（1）作AC的垂直平分线DE，交AC于点D，交AB于点E，连结CE（尺规作图，不写作法，保留作图痕迹）；
（2）在（1）所作的图中，若BC=7，AC=9，求△BCE的周长．

如图，将三角尺的直角顶点放在直线a上，a∥b，∠1=50°，∠2=60°，求∠3的度数．

三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”，如果一个“特征三角形”的“特征角”为110°，那么这个“特征三角形”的最小内角的度数为_______________．

将一副三角板如图放置，使等腰直角三角板DEF的锐角顶点D放在另一块直角三角板（∠B=60°）的斜边AB上，两块三角板的直角边交于点M．如果∠BDE=75°，那么∠AMD的度数是_______________．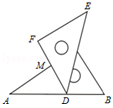

如图是一张直角三角形的纸片，两直角边AC=6cm，BC=8cm，现将△ABC折叠，使点B与点A重合，折痕为DE，则DE=______________cm．

若△ABC的三个内角满足，则这个三角形是___________三角形．

请写出定理：“等腰三角形的两个底角相等”的逆定理_______________．

如图，一副分别含有30°和45°角的两个直角三角板，拼成如下图形，其中∠C=90°，∠B=45°，∠E=30°，则∠BFD的度数是（   ）

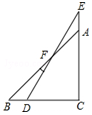
A．15°

B．25°

C．30°

D．10°

如图1是玩具拼图模板的一部分，已知△ABC的六个元素，则下面甲、乙、丙三个三角形中能和△ABC完全重合的是（   ）

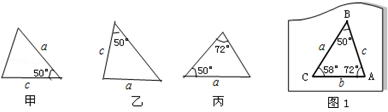
A．甲和丙

B．丙和乙

C．只有甲

D．只有丙

已知AD是△ABC的中线，BE是△ABD的中线，若△ABC的面积为20，则△ABE的面积为（   ）

A．5

B．10

C．15

D．18