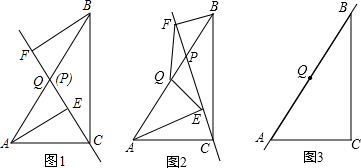
已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系式 ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.

(1)折叠后,DC的对应线段是 ,CF的对应线段是 ;
(2)△EBF是等腰三角形吗?请说明理由;
(3)若AB=4,AD=8,求△EBF的面积.
如图,△ABC是等边三角形,点D、E分别是BC、CA的延长线上的点,且CD=AE,DA的延长线交BE于点F.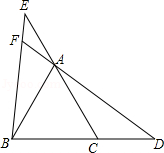
(1)求证:AD=BE;
(2)求∠BFD的度数.
已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.
求证:AD=AE.
按要求尺规作图:(不写作法,保留作图痕迹)
已知:线段a,c和∠α.如图所示.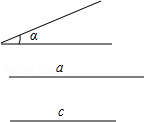
求作:△ABC,使BC=a,AB=c,∠ABC=∠α.
如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE.求证:
(1)△ABC≌△DEF;
(2)GF=GC.
如图,电信部门要在公路m,n之间的S区域修建一座电视信号发射塔P.按照设计要求,发射塔P到区域S内的两个城镇A,B的距离必须相等,到两条公路m,n的距离也必须相等.发射塔P建在什么位置?在图中用尺规作图的方法作出它的位置并标出(不写作法但保留作图痕迹).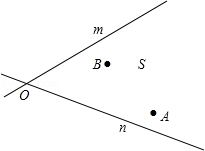
如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.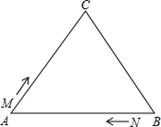
(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形?如存在,请求出此时M、N运动的时间.
如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.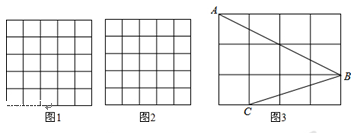
(1)在图1中以格点为顶点画一个面积为5的等腰直角三角形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、 、
、 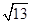 ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“趣味三角形”.
(1)请用尺规作图的方式,画一个“趣味三角形”(保留作图痕迹);
(2)如图,在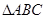 中,∠C=90°,AD是BC边上的中线,已知AC=
中,∠C=90°,AD是BC边上的中线,已知AC=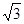 ,BC=2,请判断
,BC=2,请判断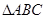 是不是“趣味三角形”,并说明理由。
是不是“趣味三角形”,并说明理由。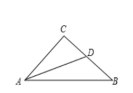
试题篮
()