如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F, DF=EF,BD=CE,过D作DG∥AC交BC于G.
求证:(1)△GDF≌△CEF;
(2)若AB=5,BC=6,求△ABC的面积.
如图,四边形ABCD的对角线AC与BD相交于点O,∠1=∠2,∠3=∠4.
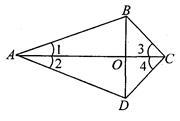
求证:(1) BC=DC; (2) AC⊥BD.
如图,△ABC中, ,
, ,AB=AC.
,AB=AC.
(1)求 的度数;
的度数;
(2)求证:BC=BD=AD.
如图,一次“台风”过后,一根旗杆被台风从离地面2.8米处吹断裂,倒下的旗杆的顶端落在离旗杆底部9.6米处,那么这根旗杆被吹断裂前有多高?(旗杆粗细、断裂磨损忽略不计)

如图,在△ABC中,CD是AB边的中线,∠CDB=60°,将△BCD沿CD折叠,使点B落在点E的位置.证明:△ADE是等边三角形.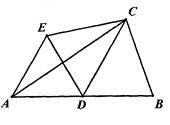
如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF, AD=BC,AD∥BC.求证:DF∥BE.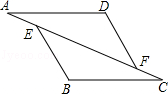
如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.求证:∠ADE=∠AED.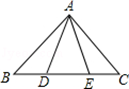
已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
如图, 于
于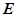 ,
, 于
于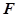 ,若
,若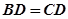 、
、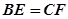 ,
,
(1)求证: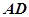 平分
平分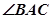 ;
;
(2)写出 与
与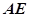 之间的等量关系,并说明理由。
之间的等量关系,并说明理由。
如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,求△ABC的周长.
如图,在Rt△ABC中,∠C=90°,DE垂直平分AB分别交BC、AB于点D、E,且CD=DE,求∠B的度数.
如图,在 中,
中, ,
, 是
是 的中点,连接
的中点,连接 .
. ,
, ,
, 是垂足.图中共有多少对全等三角形?请直接用“
是垂足.图中共有多少对全等三角形?请直接用“ ”符号把它们分别表示出来(不要求证明).
”符号把它们分别表示出来(不要求证明).
如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD= ,求AD的长.
,求AD的长.
已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,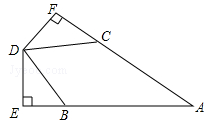
求证:DE=DF.
试题篮
()