初中数学三角形的五心解答题

如图，在正方形ABCD中，E、F分别是AB、BC上的点，且AE=BF．求证：CE=DF．

如图所示，在△ABC中，AB=AC，DE垂直平分AB于点E，交AC于点D，若△ABC的周长为26，BC=6，求△BCD的周长．

如图所示，在△ABC中，AE、BF是角平分线，它们相交于点O，AD是高，∠BAC=50°，∠C=70°，求∠DAC、∠BOA的度数．

如图，在△ABC中，AB＝BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD＝45°，AD与BE交于点F，连接CF．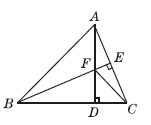

（1）求证：BF＝2AE；
（2）若CD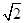＝，求AD的长．

探索与研究：
方法1：如图（a），对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得，所以
∠BAE＝90°，且四边形ACFD是一个正方形，它的面积和四边形ABFE面积相等，而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和，根据图示写出证明勾股定理的过程；
方法2：如图（b），是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的，你能根据图示再写一种证明勾股定理的方法吗？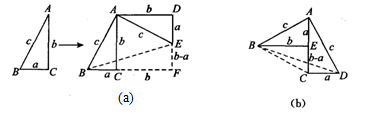

已知，如图，AB=AC，BD=CD，DE⊥AB于点E，DF⊥AC于点F，求证：DE=DF．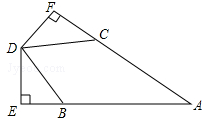

在一次消防演习中，消防员架起一架25米长的云梯AB，如图斜靠在一面墙上，梯子底端B离墙基C处7米． 

（1）求这个梯子的顶端距地面有多高？
（2）如果消防员接到命令，要求梯子的顶端A下降4米至E处（云梯长度不变），那么云梯的底部在水平方向滑动距离BF为多少米？

如图，已知在等边三角形ABC中，D是AC的中点，E为BC延长线上一点，且CE=CD，DM⊥BC，垂足为M。求证：M是BE的中点。

如图，已知△BAD和△BCE均为等腰直角三角形，∠BAD=∠BCE=90°，点M为DE的中点，过点E与AD平行的直线交射线AM于点N．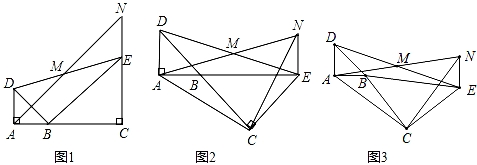

（1）当A，B，C三点在同一直线上时（如图1），求证：M为AN的中点；
（2）将图1中的△BCE绕点B旋转，当A，B，E三点在同一直线上时（如图2），求证：△ACN为等腰直角三角形；
（3）将图1中△BCE绕点B旋转到图3位置时，（2）中的结论是否仍成立？若成立，试证明之，若不成立，请说明理由．

如图，在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F．

（1）求证：△BED≌△CFD；
（2）若∠A=60°，BE=2，求△ABC的周长．

如图，已知△ABC，请用尺规过点A作一条直线，使其将△ABC分成面积相等的两部分．（保留作图痕迹，不写作法）

如图，△ABC中，AB=AC，∠BAC=90°，点D在CB上，连接AD，EA⊥AD，∠ACE=∠ABD．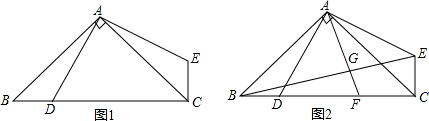

（1）求证：AD=AE；
（2）若点F为CD中点，AF交BE于点G，求∠AGE的度数．

已知：如图，△AOC≌△BOD． 求证 ：△AOD≌△BOC

如图，在兴趣活动课中，小明将一块Rt△ABC的纸片沿着直线AD折叠，恰好使直角边AC落在斜边AB上，已知∠ACB=90°．若AC=3，BC=4时．

（1）求CD的长．
（2）若AC=3，∠B=30°时，求△ABD的面积．

如图，在△ABC中，已知AB=AC，AD平分∠BAC，点M，N分别在AB，AC边上，AM=2MB，AN=2NC，
求证：DM=DN．