已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点,
(1)如图①,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
(2)如图②,若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么△DEF是否仍为等腰直角三角形?证明你的结论.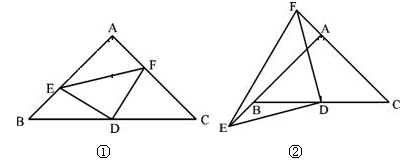
如图,△ABC是等边三角形, AE=CD,AD、BE相交于点P,BQ⊥AD于点Q.
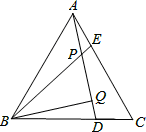
(1)试说明△ABE≌△CAD.
(2)求∠BPQ的度数.
(3)若PQ=3,PE=1, 则AD的长为 .
如图,BD平分∠MBN,A、C分别为BM、BN上的点,且BC>BA,E为BD上的一点,AE=CE,求证:∠BAE+∠BCE=180°.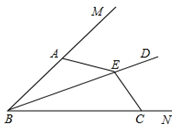
如图,C是线段AB的中点,CD∥BE,且CD=BE,求证:AD=CE.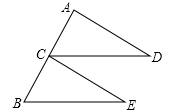
已知正方形ABCD的边长为4cm,有一动点P以1cm/s的速度沿A—B—C—D的路径运动,设P点运动的时间为 (s)(0<
(s)(0< <12),△ADP的面积为
<12),△ADP的面积为 cm2.
cm2.
(1)求 与
与 的函数关系式;
的函数关系式;
(2)在给定的平面直角坐标系中画出上述函数关系的图象; 
(3)点P运动多长时间时,△ADP是等腰三角形(只写结果).
如图,DF⊥AC于F,BE⊥AC于E,AB=CD,DF=BE.;求证:AF=CE.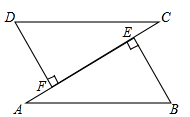
在△ABC中,∠ACB=2∠B,(1)如图①,当∠C=90°,AD为∠ABC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.请证明AB=AC+CD;
(2)①如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?请直接写出你的结论,不要求证明;
②如图③,当∠C≠90°,AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想并证明.
如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD.
已知,△ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,若E是射线CA上任意一点,DF⊥DE,交直线BC于F点.G为EF的中点,连接CG并延长交直线AB于点H.
(1)如图①,若E在边AC上.试说明:①AE=CF;②CG=GD;
(2)如图②,若E在边CA的延长线上.(1)中的两个结论是否仍成立?(直接写出成立结论的序号,不要说明理由)
(3)若AE=3,CH=5,求边AC的长.
试题篮
()