如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:
(1)FC=AD;
(2)AB=BC+AD.
如图,在△ABC中,∠B=90°,AB=6米,BC=8米,动点P以2米/秒的速度从A点出发,沿AC向点C移动,同时,动点Q以1米/秒的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止移动,设移动的时间为t秒.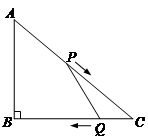
(1)①当t=2.5秒时,求△CPQ的面积;
②求△CPQ的面积S(平方米)关于时间t(秒)的函数解析式;
(2)在P、Q移动的过程中,当△CPQ为等腰三角形时,直接写出t的值;
如图,在平面直角坐标系中,O为坐标原点.△ABC的边BC在x轴上,A、C两点的坐标分别为A(0,m)、C(n,0),B(-5,0),且 ,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.
,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.
(1)求A、C两点的坐标;
(2)连接PA,用含t的代数式表示△POA的面积;
(3)当P在线段BO上运动时,在y轴上是否存在点Q,使△POQ与△AOC全等?若存在,请求出t的值并直接写出Q点坐标;若不存在,请说明理由.
这是某单位的平面示意图,已知大门的坐标为(-3,0),花坛的坐标为(0,-1).
(1)根据上述条件建立平面直角坐标系;
(2)建筑物A的坐标为(3,1),请在图中标出A点的位置.
(3)建筑物B在大门北偏东45°的方向,并且B在花坛的正北方向处,请直接写出B点的坐标.
(4)在y轴上找一点C,使△ABC是以AB腰的等腰三角形,请直接写出点C的坐标.
如图,E为正方形ABCD对角线BD上的一点,且BE=BC=1.
(1)求∠DCE的度数;
(2)点P在EC上,作PM⊥BD于M,PN⊥BC于N,求PM+PN的值.
(1)如图1, 和
和 都是等边三角形,且
都是等边三角形,且 三点共线,连接
三点共线,连接 相交于点
相交于点 ,求证:
,求证: .
.
(2)如图2,在 中,
中, °,分别以
°,分别以 和
和 为边在
为边在 外部作等边
外部作等边 、等边
、等边 和等边
和等边 ,联结
,联结 和
和 交于点
交于点 ,下列结论中正确的是 (只填序号即可)
,下列结论中正确的是 (只填序号即可)
① ;②
;② ;③
;③ °;
°;
(3)如图2,在(2)的条件下,求证: .
.

如图,在四边形 中,
中, ,
, 是
是 的中点,连接
的中点,连接 并延长交
并延长交 的延长线于点
的延长线于点 ,点
,点 在
在 边上,且
边上,且 .
.
(1)求证: ;
;
(2)连接 ,如果FM=DM,判断
,如果FM=DM,判断 与
与 的位置关系,并说明理由.
的位置关系,并说明理由.
已知:如图,在△ABC中,∠A=120°,AB=BC,D是BC边的中点,DE⊥AB,DE⊥AC,点E,F为垂足.
(1)求 、
、 的度数;
的度数;
(2)求证: ;
;
(3)求证: 是等边三角形.
是等边三角形.
已知:Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连结CD、EB.
(1)请找出图中其他的全等三角形;
(2)求证:CD=EB;
(3)求证:CF=EF.
已知:如图,在△ABC中,AB=AC,在AB,AC上分别截取相等的两条线段AD、AE,并连结BE、CD.求证:△ADC≌△AEB.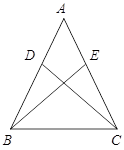
如图,点O是等边△ABC内一点,∠AOB=110º,∠BOC= ,将△BOC绕点C按顺时针方向旋转60º得△ADC,连接OD
,将△BOC绕点C按顺时针方向旋转60º得△ADC,连接OD

(1)△COD是什么三角形?说明理由;
(2)若AO= ,AD=
,AD= ,OD=
,OD= (
( 为大于1的整数),求
为大于1的整数),求 的度数
的度数
(3)当 为多少度时,△AOD是等腰三角形?
为多少度时,△AOD是等腰三角形?
如图,已知△ABC中,∠B=90°,AB=BC,BD=CE,M是AC边上的中点。
(1)求证:△DEM是等腰直角三角形.
(2)已知AD=4,CE=3,求DE的长。
试题篮
()