如图1所示,已知在△ABC和△DEF中,  ,
, .
.
(1)试说明:△ABC≌△FED的理由;
(2)若图形经过平移和旋转后得到如图2,若 ,试求∠DHB的度数;
,试求∠DHB的度数;
(3)若将△ABC继续绕点D旋转后得到图3,此时D、B、F三点在同一条直线上,若DF:FB=3:2,连结EB,已知△ABD的周长是12,且AB-AD=1,你能求出四边形ABED的面积吗?若能,请求出来;若不能,请说明理由。
如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按 的路径运动,且速度为每秒1㎝,设出发的时间为t秒.
的路径运动,且速度为每秒1㎝,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长。
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按 的路径运动,且速度为每秒2㎝,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动。当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
的路径运动,且速度为每秒2㎝,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动。当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题这种方法称为等面积法,这是一种重要的数学方法.请你用等面积法来探究下列两个问题:
(1)如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,请你用它来验证勾股定理;
(2)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC= 4,BC=3,求CD的长度.
如图,△ABC中,∠C=90°,AC=8cm,BC=4cm,一动点P从C出发沿着CB方向以1cm/S的速度运动,另一动点Q从A出发沿着AC方向以2cm/S的速度运动,P、Q两点同时出发,运动时间为t(s)。
(1)当t为几秒时,△PCQ的面积是△ABC面积的 ?
?
(2)△PCQ的面积能否为△ABC面积的一半?若能,求出t的值,若不能,说明理由。
已知:如图①,在 中,
中, ,
, ,
, ,点
,点 由
由 出发沿
出发沿 方向向点
方向向点 匀速运动,速度为1cm/s;点
匀速运动,速度为1cm/s;点 由
由 出发沿
出发沿 方向向点
方向向点 匀速运动,速度为2cm/s;连接
匀速运动,速度为2cm/s;连接 .若设运动的时间为
.若设运动的时间为 (
( ),解答下列问题:
),解答下列问题:
(1)当 为何值时,
为何值时, ?
?
(2)设 的面积为
的面积为 (
( ),求
),求 与
与 之间的函数关系式;
之间的函数关系式;
(3)是否存在某一时刻 ,使线段
,使线段 恰好把
恰好把 的周长和面积同时平分?若存在,求出此时
的周长和面积同时平分?若存在,求出此时 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(4)如图②,连接 ,并把
,并把 沿
沿 翻折,得到四边形
翻折,得到四边形 ,那么是否存在某一时刻
,那么是否存在某一时刻 ,使四边形
,使四边形 为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,以O为圆心的半圆分别与AB、AC边相切于D、E两点,且O点在BC边上,则图中阴影部分面积S阴=( )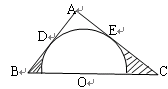
A、 B、
B、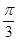
C、 5-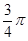 D、
D、
已知:如图,△ABC中,∠C=90°,AC=3厘米,CB=4厘米.两个动点P、Q分别从A、C两点同时按顺时针方向沿△ABC的边运动.当点Q运动到点A时,P、Q两点运动即停止.点P、Q的运动速度分别为1厘米/秒、2厘米/秒,设点P运动时间为 (秒).
(秒). 
(1)当时间 为何值时,以P、C、Q三点为顶点的三角形的面积(图中的阴影部分)等于2厘米2;
为何值时,以P、C、Q三点为顶点的三角形的面积(图中的阴影部分)等于2厘米2;
(2)当点P、Q运动时,阴影部分的形状随之变化.设PQ与△ABC围成阴影部分面积为S(厘米2),求出S与时间 的函数关系式,并指出自变量
的函数关系式,并指出自变量 的取值范围;
的取值范围;
(3)点P、Q在运动的过程中,阴影部分面积S有最大值吗?若有,请求出最大值;若没有,请说明理由.
如图,在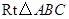 中,
中,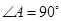 ,
,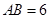 ,
,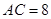 ,
,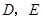 分别是边
分别是边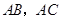 的中点,点
的中点,点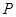 从点
从点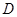 出发沿
出发沿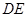 方向运动,过点
方向运动,过点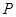 作
作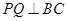 于
于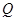 ,过点
,过点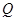 作
作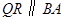 交
交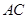 于
于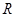 ,当点
,当点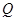 与点
与点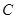 重合时,点
重合时,点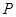 停止运动.设
停止运动.设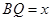 ,
,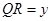 .
.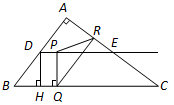
(1)求点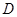 到
到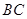 的距离
的距离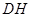 的长;
的长;
(2)求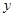 关于
关于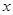 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点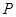 ,使
,使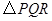 为等腰三角形?若存在,请求出所有满足要求的
为等腰三角形?若存在,请求出所有满足要求的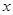 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图,点 在射线
在射线 上,点
上,点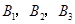 在射线
在射线 上,且
上,且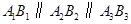 ,
,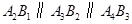 .若
.若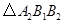 ,
,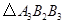 的面积分别为1,4,则图中三个阴影三角形面积之和为 .
的面积分别为1,4,则图中三个阴影三角形面积之和为 .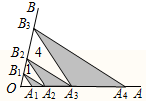
一位同学拿了两块 三角尺
三角尺 ,
, 做了一个探究活动:将
做了一个探究活动:将 的直角顶点
的直角顶点 放在
放在 的斜边
的斜边 的中点处,设
的中点处,设 .
.
(1)如图(1),两三角尺的重叠部分为 ,则重叠部分的面积为 ,周长为 .
,则重叠部分的面积为 ,周长为 .
(2)将图(1)中的 绕顶点
绕顶点 逆时针旋转
逆时针旋转 ,得到图26(2),此时重叠部分的面积为 ,周长为 .
,得到图26(2),此时重叠部分的面积为 ,周长为 .
(3)如果将 绕
绕 旋转到不同于图(1)和图(2)的图形,如图(3),请你猜想此时重叠部分的面积为 .
旋转到不同于图(1)和图(2)的图形,如图(3),请你猜想此时重叠部分的面积为 .
(4)在图(3)情况下,若 ,求出重叠部分图形的周长.
,求出重叠部分图形的周长.
已知△ 中,
中, (如图),点
(如图),点 到
到 两边的距离相等,且
两边的距离相等,且 .
.
(1)先用尺规作出符合要求的点 (保留作图痕迹,不需要写作法),然后判断△
(保留作图痕迹,不需要写作法),然后判断△ 的形状,并说明理由;
的形状,并说明理由;
(2)设 ,
, ,试用
,试用 、
、 的代数式表示
的代数式表示 的周长和面积;
的周长和面积;
(3)设 与
与 交于点
交于点 ,试探索当边
,试探索当边 、
、 的长度变化时,
的长度变化时, 的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
如图,在△ABC中,BC="8" cm,BP、CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是___________cm。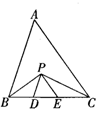
如图所示,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论中:①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC,正确的是 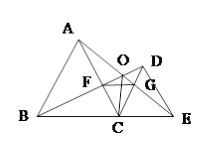
试题篮
()