(1)如图1, 为
为 的角平分线,
的角平分线, 于
于 ,
, 于
于 ,
, ,请补全图形,并求
,请补全图形,并求 与
与 的面积的比值;
的面积的比值;
(2)如图2,分别以 的边
的边 、
、 为边向外作等边三角形
为边向外作等边三角形 和等边三角形
和等边三角形 ,
, 与
与 相交于点
相交于点 ,判断
,判断 与
与 的数量关系,并证明;
的数量关系,并证明;
(3)在四边形 中,已知
中,已知 ,且
,且 ,对角线
,对角线 平分
平分 ,
,
请直接写出 和
和 的数量关系.
的数量关系.
如图,在等腰梯形ABCD中,∠B=60º,且AB=AD=CD,请你将等腰梯形分成3个三角形,
使得其中有两个是相似三角形,且相似比不为1.
现在请你参考示意图,另外再给出三种分割方法(注:在两个相似三角形中标明必要的角度.)


已知△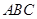 中,点
中,点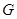 是△
是△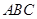 的重心,过点
的重心,过点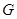 作
作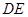 ∥
∥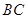 ,与
,与 相交于点
相交于点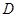 ,与
,与 相交于点
相交于点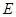 ,如果△
,如果△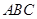 的面积为9.那么△
的面积为9.那么△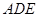 的面积是 .
的面积是 .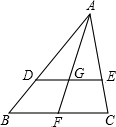
如图,直线 与
与 轴负半轴、
轴负半轴、 轴正半轴分别交于A、B两点,正比例函数
轴正半轴分别交于A、B两点,正比例函数 的图像与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM =10,BN =3,
的图像与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM =10,BN =3,
(1)求A、B两点的坐标;(用b表示)
(2)图中有全等的三角形吗?若有,请找出并说明理由。
(3)求MN的长.
如图所示,∠BAC=∠ABD=90°,AC=BD,点O是AD,BC的交点,点E是AB的中点.
(1)图中有哪几对全等三角形?请写出来;
(2)试判断OE和AB的位置关系,并给予证明.
(1)如图1,在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE= ∠ABC(0°<∠CBE<
∠ABC(0°<∠CBE< ∠ABC)。以点B为旋转中心,将△BEC按逆时针方向旋转∠ABC,得到△BE’A(点C与点A重合,点E到点E’处),连接DE’。求证:DE’="DE."
∠ABC)。以点B为旋转中心,将△BEC按逆时针方向旋转∠ABC,得到△BE’A(点C与点A重合,点E到点E’处),连接DE’。求证:DE’="DE."
(2)如图2,在△ABC中,BA=BC,∠ABC=90°,D,E是AC边上的两点,
且满足∠DBE= ∠ABC(0°<∠CBE<45°).求证:DE2=AD2+EC2.
∠ABC(0°<∠CBE<45°).求证:DE2=AD2+EC2.
如图,Rt△AB ¢C ¢是由Rt△ABC绕点A顺时针旋转得到的,连结CC ¢交斜边于点E,CC ¢的延长线交BB ¢于点F.
(1)证明:△ACE∽△FBE;
(2)设∠ABC= ,∠CAC ¢ =
,∠CAC ¢ = ,试探索
,试探索 、
、 满足什么关系时,△ACE与△FBE是全等三角形,并说明理由.
满足什么关系时,△ACE与△FBE是全等三角形,并说明理由.
如图,在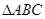 中,AB = AC,D是底边BC的中点,作DE⊥AB于E,DF⊥AC于F,
中,AB = AC,D是底边BC的中点,作DE⊥AB于E,DF⊥AC于F,
求证:DE = DF.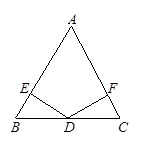
证明: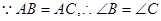 (① )
(① )
在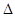 BDE和
BDE和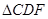 中,
中,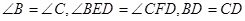 ,
,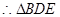 ≌
≌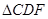 (② )
(② )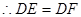 (③ )
(③ )
⑴上面的证明过程是否正确?若正确,请写出①、②和③的推理根据.
⑵请你写出另一种证明此题的方法.
两个大小相同且含30°角的三角板ABC和DEC如图(1)摆放,使直角顶点重合.将图(1)中△DEC绕点C逆时针旋转30°得到图(2),点F、G分别是CD、DE与AB的交点,点H是DE与AC的交点.
(1)不添加辅助线,写出图(2)中所有与△BCF全等的三角形;
(2)将图(2)中的△DEC绕点C逆时针旋转45°得△D1E1C,点F、G、H的对应点分别为F1、G1、H1,如图(3),探究线段D1F1与AH1之间的数量关系,并写出推理过程;
(3)在(2)的条件下,若D1E1与CE交于点I,求证:G1I=CI.
一副直角三角板叠放如图所示,现将含45°角的三角板ADE固定不动,把含30°角的三角板ABC绕顶点A顺时针旋转角α (α =∠BAD且0°<α<180°),使两块三角板至少有一组边平行.
(1)如图①,α =____°时,BC∥DE;
(2)请你分别在图②、图③的指定框内,各画一种符合要求的图形,标出α,并完成各项填空:
图②中,α = °时,有 ∥ ; 图③中,α = °时,有 ∥ .

如图,在 中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是( )
中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是( )
| A.4.8 | B.4.75 | C.5 | D. |

阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两 腰的距离分别为 ,腰上的高为h,连结AP,则
,腰上的高为h,连结AP,则 ,即:
,即: ,
, (1)理解与应用
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在 三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为 ,
, ,
, ,试证明:
,试证明: .
.

(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于 ;
(3)拓展与延伸
若边长为2的正n边形A1A2…An内部任意一点P到各边的距离为 ,请问
,请问 是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值。
是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值。
为了探索代数式 的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作
的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作 ,连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则
,连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则 ,
, 则问题即转化成求AC+CE的最小值.
则问题即转化成求AC+CE的最小值.
(1)我们知道当A、C、E在同一直线上时, AC+CE的值最小,于是可求得 的最小值等于 ,此时
的最小值等于 ,此时 ;
;
(2)请你根据上述的方法和结论,试构图求出代数式 的最小值.
的最小值.
如图,已知抛物线y=-x2+2x+3交x轴于A、B两点(点A在点B的左侧),与y轴交于点C。
(1)求点A、B、C的坐标。
(2)若点M为抛物线的顶点,连接BC、CM、BM,求△BCM的面积。
(3)连接AC,在x轴上是否存在点P使△ACP为等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由。
试题篮
()