初中数学三角形的五心试题

对于下列命题：
①对顶角相等；②同位角相等；③两直角相等； ④邻补角相等；
⑤有且只有一条直线垂直于已知直线；　　
⑥三角形一边上的中线把原三角形分成面积相等的两个三角形.
其中是真命题的共有

A．2个

B．3个

C．4个

D．5个

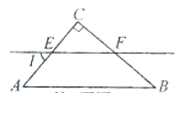
如图，在Rt△ABC中，∠ACB=90°，，CM是斜边AB的中线，将△ACM沿直线CM折叠，点A落在点D处，如果CD恰好与AB垂直，那么∠A=_____________.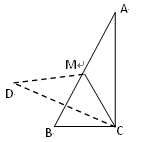

已知：在△ABC中，∠CAB=，且，AP平分∠CAB．

（1）如图1，若，∠ABC=32°，且AP交BC于点P，试探究线段
AB，AC与PB之间的数量关系，并对你的结论加以证明；
答：线段AB，AC与PB之间的数量关系为：___________________________．

（2）如图2，若∠ABC=，点P在△ABC的内部，且使∠CBP=30°，
求∠APC的度数（用含的代数式表示）．

(本小题满分1 0分)
如图，已知线段AB∥CD，AD与B C相交于点K，E是线段AD上一动点。

(1)若BK=KC，求的值；
(2)连接BE，若BE平分∠ABC，则当AE= AD时，猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明．再探究：当AE=AD (n>2)，而其余条件不变时，线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论，不必证明．

如图，△ABC中，∠ACB = 90°，AC=BC=1，取斜边中点，向斜边做垂线，画出一个新的等腰直角三角形，此时这个三角形的斜边与BC垂直.如此继续下去，直到所画直角三角形的斜边再次与△ABC的BC边垂直为止，此时这个三角形的直角边长为          .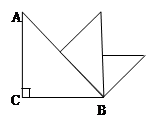

（第18题）     

（本小题满分8分）要在宽为28m的南滨路的路边安装路灯。路灯的灯臂长AC为3m，且与灯柱AB成120°的夹角（如图所示），路灯采用圆锥形灯罩，灯罩的轴线CD与灯臂AC垂直。当灯罩的轴线通过公路路面的中线时，照明效果最理想。问：应设计多高的灯柱，才能取得最理想的照明效果？（精确到0.01m，）
 

如图，是一段平直的铁轨，某天小明站在距离铁轨100米的A处，他发现一列火车从左向右自远方驶来，已知火车长200米，设火车的车头为B点，车尾为C点，小明站着不动，则从小明发现火车到火车远离他而去的过程中，以A、B、C三点为顶点的三角形是等腰三角形的时刻共有（　　）
 
A.2个       B.3个      C.4个      D.5个

如图是由9个等边三角形拼成的六边形，已知中间最小的等边三角形的边长为1，则这个六边形的周长是        (17届江苏初一1试)如图   如              .

已知：将一副三角板(Rt△ABC和Rt△DEF)如图①摆放，点E、A、D、B在一条直线上，且D是AB的中点。将Rt△DEF绕点D顺时针方向旋转角α(0°＜α＜90°)，在旋转过程中，直线DE、AC相交于点M，直线DF、BC相交于点N，分别过点M、N作直线AB的垂线，垂足为G、H.
当α＝30°时，DF刚好过点C(如图②)，求证：AM=DM；
在（1）的条件下，试判断线段AG与DH的数量关系，并说明理由；
“当在Rt△DEF绕点D顺时针方向旋转过程中时α=60°(如图③)，(2)中的结论是否成立？

『问题情境』勾股定理是一条古老的数学定理，它有多种证明方法，我国汉代数学家赵爽根据弦图，利用面积法进行了证明．著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球，作为地球人与其它星球“人”进行第一次“谈话”的语言．
『定理表述』请你根据图1中的直角三角形叙述勾股定理(用文字及符号语言叙述)．

『尝试证明』以图1中的直角三角形为基础，可以构造出以a、b为底，以a＋b为高的直角梯形(如图2)，请你利用图2，验证勾股定理．

『知识拓展』利用图2中的直角梯形，我们可以证明＜．其证明步骤如下：
∵BC＝a＋b，AD＝         ，
又在直角梯形ABCD中，BC    AD(填大小关系)，
即                     ．
∴＜．

(本题12分)数学课上，李老师出示了如下框中的题目.

小敏与同桌小聪讨论后，进行了如下解答：
（1）特殊情况，探索结论
当点为的中点时，如图1，确定线段与的大小关系，请你直接写出结论：
       （填“>”,“<”或“=”）.

图2

图1

（2）特例启发，解答题目
解：题目中， 与 的大小关系是：    （填“>”,“<”或“=”）.理由如下：如图2，过点 作 ，交 于点 .
（请你完成以下解答过程）
（3）拓展结论，设计新题
在等边三角形 中，点 在直线 上，点 在直线 上，且 .若 的边长为1， ，求 的长（请你直接写出结果）.

若从矩形一边上的点到对边的视角是直角，即称该点是直角点。例如，如图的矩形中，点在边上，连接，,则点为直角点。若点分别为矩形的边上的直角点，且,,则的长为     

直角三角形一直角边长为11，另两条边长均为自然数，则其周长为_________.

已知△ABC中，AB=；BC=6；CA=.点M是BC中点，过点B作AM延长线的垂线，垂足为D，则线段BD的长度是         .

下面是六个推断：
①因为平角的两条边在一条直线上，所以直线是一个平角；
②因为周角的两条边在一条射线上，所以射线是一个周角；
③因为扇形是圆的一部分，所以圆周的一部分是扇形；
④因为平行的线段没有交点，所以不相交的两条线段平行；
⑤因为正方形的边长都相等，所以边长相等的四边形是正方形；
⑥因为等腰三角形有两个内角相等，所以有两个内角相等的三角形是等腰三角形；
其中正确的结论有  , 个，其序号是    ；