如图,△ABC≌△ADE且∠ABC=∠ADE,∠ACB=∠AED,BC.DE交于点O.则下列四个结论中,①∠1=∠2;②BC=DE;③△ABD∽△ACE;④A.O、C.E四点在同一个圆上,一定成立的有( )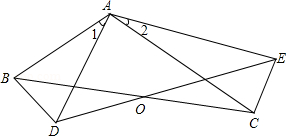
A. 1个 B. 2个 C. 3个 D. 4个
已知实数x,y满足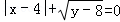 ,则以x,y的值为两边长的等腰三角形的周长是( )
,则以x,y的值为两边长的等腰三角形的周长是( )
| A.20或16 | B.20 | C.16 | D.以上答案均不对 |
如图,等边三角形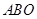 放在平面直角坐标系中,其中点
放在平面直角坐标系中,其中点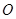 为坐标原点,点
为坐标原点,点 的坐标为(
的坐标为(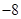 ,
, ),点
),点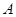 位于第二象限.已知点
位于第二象限.已知点 、点
、点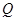 同时从坐标原点出发,点
同时从坐标原点出发,点 以每秒
以每秒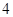 个单位长度的速度沿
个单位长度的速度沿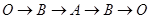 来回运动一次,点
来回运动一次,点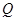 以每秒
以每秒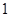 个单位长度的速度从
个单位长度的速度从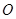 往
往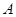 运动,当点
运动,当点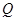 到达点
到达点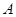 时,
时, 、
、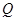 两点都停止运动.在点
两点都停止运动.在点 、点
、点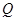 的运动过程中,存在某个时刻,使得
的运动过程中,存在某个时刻,使得 、
、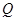 两点与点
两点与点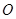 或点
或点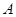 构成的三角形为直角三角形,那么点
构成的三角形为直角三角形,那么点 的坐标为__________.
的坐标为__________.
课本中,把长与宽之比为 的矩形纸片称为标准纸.请思考解决下列问题:
的矩形纸片称为标准纸.请思考解决下列问题:
(1)将一张标准纸ABCD(AB<BC)对开,如图1所示,所得的矩形纸片ABEF是标准纸.请给予证明.
(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:
第一步:沿过A点的直线折叠,使B点落在AD边上点F处,折痕为AE(如图2甲);
第二步:沿过D点的直线折叠,使C点落在AD边上点N处,折痕为DG(如图2乙),此时E点恰好落在AE边上的点M处;
第三步:沿直线DM折叠(如图2丙),此时点G恰好与N点重合.
请你探究:矩形纸片ABCD是否是一张标准纸?请说明理由.
(3)不难发现:将一张标准纸按如图3一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD,AB=1,BC= ,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.
,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.
如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE,那么DE长的最小值是 ▲ .
如图7,在△ABC中,AB=AC=5,BC=6,点E、F分别在AB、BC边上,将△BEF沿直线EF翻折后,点B落在对边AC的点为B',若△B'FC与△ABC相似,那么BF= .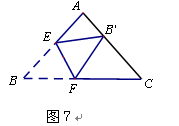
如图,AB∥CD,∠BAC与∠DCA的平分线相交于点G,GE⊥AC于点E,F为AC上的一点,且FA=FG=FC,GH⊥CD于H.下列说法:①AG⊥CG;②∠BAG=∠CGE;③S△AFG=S△CFG;④若∠EGH:∠ECH=2:7,则∠EGF=50度.其中正确的有( )
| A.①②③④ | B.②③④ | C.①③④ | D.①②④ |
如图所示,当小华站立在镜子 前
前 处时,他看自己的脚在镜中的像的俯角为
处时,他看自己的脚在镜中的像的俯角为 ;如果小华向后退0.5米到
;如果小华向后退0.5米到 处,这时他看自己的脚在镜中的像的俯角为
处,这时他看自己的脚在镜中的像的俯角为 .求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据:
.求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据: )
)
两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O为边
AC和DF的交点.不重叠的两部分△AOF与△DOC是否全等?为什么?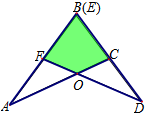
如图11-1,是我们平时使用的等臂圆规,即CA=CB.若n个相同规格的等臂圆规的两脚依次摆放在同一条直线上如图2所示,其张角度数变化如下:∠A1C1A2=160°,∠A2C2A3=80°,∠A3C3A4=40°,∠A4C4A5=20°,…. ,根据上述规律请你写出∠AnCnAn+1=_______________°.(用含n的代数式表示)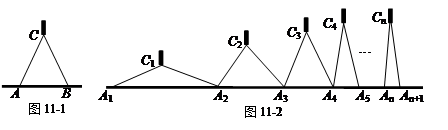
如图,点A1、B1、C1分别是△ABC的三边BC、AC、AB的中点,点A2、B2、C2分别是△A1B1C1的边B1C1、A1C1、A1B1的中点,依此 类推,则△AnBnCn与△ABC的面积比为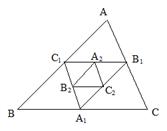
如图,△ABC中,AB=4,BC=3,AC=5. 以AB所在直线为轴旋转一周形成的几何体的侧面积为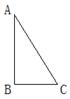
在一次数学活动课上,老师组织大家利用矩形进行图形变换的探究活动.第一小组同学将矩形纸片ABCD按如下顺序进行操作:对折、展平,得折痕EF(如图1);再沿GC折叠,使点B落在EF上的点B'处(如图2),这样能得到∠B'GC的大小,你知道∠B'GC的大小是多少吗?请写出求解过程.

第二小组的同学,在一个矩形纸片上按照图3的方式剪下△ABC,其中BA=BC,将△ABC沿着直线AC的方向依次进行平移变换,每次均移动AC的长度,得到了△CDE、△EFG和△GHI,如图4.已知AH=AI,AC长为a,现以AD、AF和AH为三边构成一个新三角形,已知这个新三角形面积小于15,请你帮助该小组求出a可能的最大整数值.

探究活动结束后,老师给大家留下了一道探究题:如图5,已知AA'=BB'=CC'=2,∠AOB'=∠BOC'=∠COA'=60°,请利用图形变换探究S△AOB'+S△BOC'+S△COA'与的大小关系.

试题篮
()