如图,△ABC中,E为AD与CF的交点,AE=ED,已知△ABC的面积是1,△BEF的面积是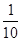 ,则△AEF的面积是---;
,则△AEF的面积是---;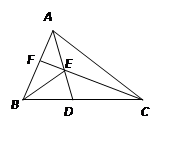
如图所示,一个正方形水池的四周恰好被4个正n边形地板砖铺满,则n等于( )
| A.4 | B.6 | C.8 | D.10 |
若一个三角形的三条边的长是a,b,c,并且满足恒等式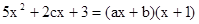 ,则这个三角形是( )
,则这个三角形是( )
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.等边三角形 |
两个直角三角形如图放置,则∠BFE与∠CAF的度数之比等于( )
| A.8 | B.9 | C.10 | D.11 |
已知等边△ABC和Rt△DEF按如图所示的位置放置,点B,D重合,且点E、B(D)、
C在同一条直线上.其中∠E=90°, 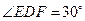 ,
,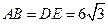 ,现将△DEF
,现将△DEF
沿直线BC以每秒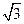 个单位向右平移,直至E点与C 点重合时停止运动,设运动时
个单位向右平移,直至E点与C 点重合时停止运动,设运动时
间为t秒.
(1) 试求出在平移过程中,点F落在△ABC的边上时的t值;
(2) 试求出在平移过程中△ABC和Rt△DEF重叠部分的面积s与t的函数关系式;
(3) 当D与C重合时,点H为直线DF上一动点,现将△DBH绕点D顺时针旋转60°得到
△ACK,则是否存在点H使得△BHK的面积为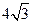 ,若存在,试求出CH的值;若不存在,请说明理由.
,若存在,试求出CH的值;若不存在,请说明理由.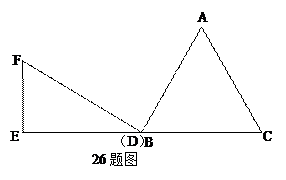

如图,在△ABC中,∠A=a,∠ABC的平分线与∠ACD的平分线交于点A1,得∠A1;∠A1BC的平分线与∠A1CD的平分线交于点A2,得∠A2;…;∠A2008BC的平分线与∠A2008CD的平分线交于点A2009;得∠A2009;则
∠A2009=__________.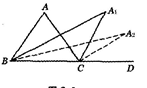
如图,△ABC中,AB=AC,∠BAC=40°,D为△ABC内一点,如果将△ACD绕点A按逆时针方向旋转到△ABD′的位置,则∠ADD′的度数是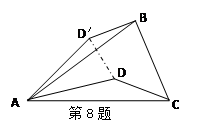
| A.40° | B.50° | C.60° | D.70° |
如图,在直线 上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1.0,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+S2+S3+S4= .
上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1.0,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+S2+S3+S4= .
已知第一个三角形的周长为1,它的三条中位线组成第二个三角形,第二个三角形的三条中位线又组成第三个三角形,以此类推,则第2003个三角形的周长为( )
A. |
B. |
C.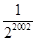 |
D.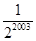 |
(本小题满分8分)
已知如图,点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AC∥DF.
求证:(1)△ABC≌△DEF;(2)BE=CF.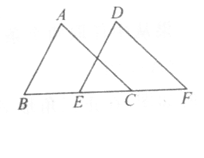
已知:在△ABC中,BC=a,AC=b,以AB为边作等边三角形ABD. 探究下列问题:
(1)如图1,当点D与点C位于直线AB的两侧时,a=b=3,且∠ACB=60°,则CD= ;
(2)如图2,当点D与点C位于直线AB的同侧时,a=b=6,且∠ACB=90°,则CD= ;
(3)如图3,当∠ACB变化,且点D与点C位于直线AB的两侧时,求 CD的最大值及相应的∠ACB的度数.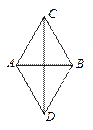

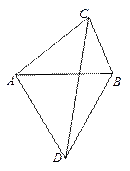
图1 图2 图3
已知在△ABC中,BC=a.如图1,点B1 、C1分别是AB、AC的中点,则线段B1C1的长是_______;
如图2,点B1 、B2 ,C1 、C2分别是AB 、AC的三等分点,则线段B1C1 + B2C2的值是__________;
如图3, 点 ,
, 分别是AB、AC的(n+1)等分点,则线段B1C1 + B2C2+……+ BnCn的值是 ______.
分别是AB、AC的(n+1)等分点,则线段B1C1 + B2C2+……+ BnCn的值是 ______. 
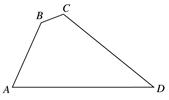
如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=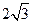 ,BC=
,BC=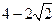 ,CD=
,CD= ,则AD边的长为( ).
,则AD边的长为( ).
A.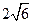 |
B.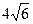 (第3题) |
C.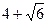 |
D.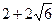 |
把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG.
(1)求证:△BHE≌△DGF;
(2)若AB=6cm,BC=8cm,求线段FG的长.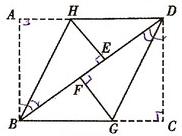
试题篮
()