如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)△AOD能否为等边三角形?为什么?
(4)探究:当α为多少度时,△AOD是等腰三角形.
如图所示,某船上午11时30分在A处观测海岛B在北偏东60°方向,该船以每小时10海里的速度航行到C处,再观测海岛B在北偏东30°方向,又以同样的速度继续航行到D处,再观测海岛在北偏西30°方向,当轮船到达C处时恰好与海岛B相距20海里,请你确定轮船到达C处和D处的时间.
如图1,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的异侧,BD⊥AE于点D,CE⊥AE于点E.
(1)求证:BD=DE+CE;
(2)若直线AE绕点A旋转到图2位置时(BD<CE),其余条件不变,问BD与DE,CE的关系如何,请证明;
(3)若直线AE绕点A旋转到图3时(BD>CE),其余条件不变,BD与DE,CE的关系怎样?请直接写出结果,不须证明.
如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,PQ=4,PE=1.
(1)求证:∠BPQ=60°(提示:利用三角形全等、外角的性质)
(2)求BE的长.
如图所示,已知点A,F,E,C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.
如图,在平面直角坐标系中,OA=OB=OC=8,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的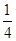 .
.
(1)求点D的坐标;
(2)过点C作CE⊥AD,交AB交于F,垂足为E.求证:OF=OG;
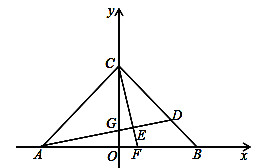
(3)若点F的坐标为(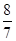 ,0),在第一象限内是否存在点P,使△CFP是以CF为腰长的等腰直角三角形?若存在,请求出点P坐标;若不存在,请说明理由.
,0),在第一象限内是否存在点P,使△CFP是以CF为腰长的等腰直角三角形?若存在,请求出点P坐标;若不存在,请说明理由.
如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.
在同一直角坐标系中分别描出点A(-3,0)、B(2,0)、C(1,3),再用线段将这三点首尾顺次连接起来,求△ABC的面积与周长.
利用网格线画图:如图,点A、B、C都在正方形网格的格点上.
(1)在BC上找一点P,使PA=PB;
(2)在BC上找一点Q,使点Q到AB和AC的距离相等.
试题篮
()