初中数学三角形的五心解答题

如图是一块地的平面图，其中AD=4m，CD=3m，AB=13m，BC=12m,∠ADC=90°，求这块地的面积．

如图，已知一块四边形的草地ABCD，其中∠A=60°，∠B=∠D=90°，AB=20米，CD=10米，求这块草地的面积．

如图，边长为4的等边△AOB的顶点O在坐标原点，点A在x轴正半轴上，点B在第一象限．一动点P沿x轴以每秒1个单位长度的速度由点O向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒．在点P的运动过程中，线段BP的中点为点E，将线段PE绕点P按顺时针方向旋转60º得PC．

（1）当点P运动到线段OA的中点时， 点C的坐标为         ；
（2）在点P从点O到点A的运动过程中，用含t的代数式表示点C的坐标；
（3）在点P从点O到点A的运动过程中，求出点C所经过的路径长．

如图，点A是5×5网格图形中的一个格点，图中每个小正方形的边长为1，请在网格中按下列要求操作：

（1）以点A为其中的一个顶点，在图（1）中画一个面积等于3的格点直角三角形；
（2）以点A为其中的一个顶点，在图（2）中画一个面积等于的格点等腰直角三角形．

如图，长方形纸片中，AB=10，将纸片折叠，使顶点落在边上的点处，折痕的一端点在边上．


图（2）
（1）如图（1），当折痕的另一端在边上且AE=5时，求AF的长
（2）如图（2），当折痕的另一端在边上且BG=13时，求AF的长．

如图，△ACB和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°，D为AB边上一点．求证：

（1）；
（2）．

如图，已知在△ABC中，CD⊥AB于D，AC＝20，BC＝15，AD＝16．

（1）求AB的长；
（2）问△ABC是直角三角形吗？请说明理由．

如图，在△ABC中，AB=AC，点D、E、F分别在AB、BC、AC边上，且BE=CF，BD=CE．

（1）求证：DE=EF；
（2）当∠A=50°时，求∠DEF的度数；

如图，已知在等腰直角三角形△DBC中，∠BDC=90°，BF平分∠DBC，与CD相交于点F，延长BD到A，使DA=DF，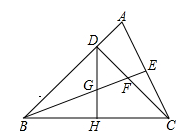

（1）试说明：△FBD≌△ACD；
（2）延长BF交AC于E，且BE⊥AC，试说明：CE＝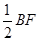

已知，如图，四边形ABCD，∠A=∠B=Rt∠

（1）用直尺和圆规，在线段AB上找一点E，使得EC=ED，连接EC，ED（不写作法，保留作图痕迹）
（2）在（1）的图形中，若∠ADE=∠BEC，且CE=3，BC=，求AD的长．

如图，△ABC是边长为4cm的等边三角形，AD为BC边上的高，点P沿BC向终点C运动，速度为1cm/s，点Q沿CA、AB向终点B运动，速度为2cm/s，若点P、Q两点同时出发，设它们的运动时间为x（s）．

（l）求x为何值时，PQ⊥AC；x为何值时，PQ⊥AB？
（2）当O＜x＜2时，AD是否能平分△PQD的面积？若能，说出理由；
（3）探索以PQ为直径的圆与AC的位置关系，请写出相应位置关系的x的取值范围（不要求写出过程）．

如图，已知四边形ABCD是平行四边形，DE⊥AB，DF⊥BC，垂足分别是E、F，且DE=DF．

（1）求证：△ADE≌△CDF；
（2）判断四边形ABCD的形状，并说明理由．

如图1，矩形ABCD中，AB=4，AD=3，把矩形沿直线AC折叠，使点B落在点E处，AE交CD于点F，连接DE．

（1）求证：△DEC≌△EDA；
（2）求DF的值；
（3）如图2，若P为线段EC上一动点，过点P作△AEC的内接矩形，使其顶点Q落在线段AE上，定点M、N落在线段AC上，当线段PE的长为何值时，矩形PQMN的面积最大？并求出其最大值．

如图，已知△ABC中，AB=AC=10厘米，BC=8厘米，点D为AB的中点．如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动．当一个点停止运动时时，另一个点也随之停止运动．设运动时间为t．

（1）若Q的运动速度与P的速度相等，经过多少秒后？△BPD与△CQP全等．
（2）若Q的速度与点P的速度不相等，当Q的速度为多少时，能够使△BPD与△CQP全等？

为了丰富少年儿童的业余生活，某社区要在如图所示AB所在的直线上建一图书室E，并使图书室E到本社区两所学校C和D的距离相等（C．D所在位置如图所示），CA⊥AB于A，DB⊥AB于B．已知AB=25km，CA=15km，DB=10km．

（1）请用尺规在图中作出点E；    
（2）求图书室E与点A的距离．