如图,在△ABC中,∠BAC=90°,AB=6cm,BC=10cm,点D在线段AC上,且CD=2cm,动点P从BA的延长线上距A点10cm的E点出发,以每秒2cm的速度沿射线EA的方向运动了t秒.

(1)求AD的长.
(2)直接写出用含有t的代数式表示PE= .
(3)在运动过程中,是否存在某个时刻,使△ABC与△ADP全等?若存在,请求出t值;若不存在,请说明理由.
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.
图①是一面矩形彩旗完全展平时的尺寸图(单位:cm),其中矩形ABCD是由双层白布缝制的穿旗杆用的旗裤,阴影部分DCEF为矩形绸缎旗面.
(1)用经加工的圆木杆穿入旗裤作旗杆,求旗杆的最大直径(精确到1cm);
(2)将穿好彩旗的旗杆垂直插在操场上,旗杆从旗顶到地面的高度为220cm,在无风的天气里,彩旗自然下垂,如图②,求彩旗下垂时最低处离地面的最小高度h.
如图,△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,求△ABC的周长.
如图,在Rt△ABC中,∠C=90°,DE垂直平分AB分别交BC、AB于点D、E,且CD=DE,求∠B的度数.
如图,在△ABC中,AB=AC,D是BC的中点,连接AD.DE⊥AB,DF⊥AC,E,F是垂足.图中共有多少对全等三角形?请直接用“≌”符号把它们分别表示出来.(不要求证明)
如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”。如图,在三角形ABC中,∠C=90°,较短的一条直角边BC=1,且三角形ABC是“有趣三角形”,求三角形ABC的“有趣中线”的长。
如图(1),等边△ABC中,D是AB边上的动点,以CD为一边,向上作等边△EDC,连接AE.
(1)求证:AE∥BC;
(2)如图(2),将(1)中的动点D运动到边BA的延长线上,仍作等边△EDC,请问是否仍有AE∥BC?证明你的猜想.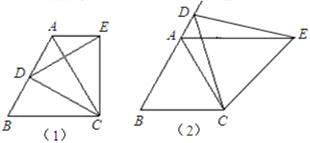
已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明你的结论.
如图,在等腰△ABC中,AB=AC,以B点为圆心,BC长为半径画弧,分别交AC、AB于D、E两点,并连接BD、DE.若∠A=20°,试求∠BDE的度数.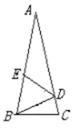
阅读课本材料,解答后面的问题.
折纸与证明
折纸,常常能为证明一个命题提供思路和方法.例如,在△ABC中,AB>AC(图27-1),怎样证明∠C>
∠B呢?
把AC沿∠A的平分线AD翻折,因为AB>AC,所以,点C落在AB上的点C’处(图27-2).于是,由∠AC’D>∠B,可得∠C>∠B.
在△ABC中,∠B=2∠C,点D为线段BC上一动点,当AD满足某种条件时,探讨在线段AB、BD、CD、AC四条线段中,某两条或某三条线段之间存在的数量关系.
(1)如图3,当AD⊥BC时,求证:AB+BD=DC;
(2)如图4,当AD是∠BAC的角平分线时,写出AB、BD、AC的数量关系,并证明.
如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F, DF=EF,BD=CE,过D作DG∥AC交BC于G.
求证:(1)△GDF≌△CEF;
(2)若AB=5,BC=6,求△ABC的面积.
试题篮
()