如图7,已知AB、AC分别为⊙O的直径和弦,D为⌒BC的中点,DE⊥AC于E,DE=6,AC=16.求证:DE是⊙O的切线.
求直径AB的长.

已知:如图,∠MAN=45°,B为AM上的一个定点.若点P在射线AN上,以P为圆心,PA为半径的圆与射AN的另一个交点为C.请确定⊙P的位置,使BC恰与⊙P相切.
画出⊙P;(不要求尺规作图,不要求写画法)
连结BC、BP并填空:
①∠ABC=______°;
②比较大小:∠ABP______∠CBP.(用“>”、“<”或“=”连接)
如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O于D,AD的延长线交BC于E,若∠C = 25°,求∠A的度数.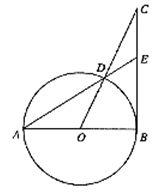
在平面直角坐标系xOy中,已知直线l1经过点A(-2,0)和点B(0, ),直线l2的函数表达式为
),直线l2的函数表达式为 ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.求直线l1的函数表达式;
当⊙C和直线l2相切时,请证明点P到直线CM的距离等于⊙C的半径R,并写出R=
 时a的值.
时a的值.当⊙C和直线l2不相离时,已知⊙C的
 半径R=
半径R= ,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.

一座拱型桥,桥下水面宽度AB是20米,拱高CD是4米.若水面上升3米至EF,则水面宽度EF是多少?若把它看作是抛物线的一部分,在坐标系中(如图1)可设抛物线的表达式为
 .
.
请你填空:a= ,c= ,EF= 米.若把它看作是圆的一部分,则可构造图形(如图2)计算如下:
设圆的半径是r米,在Rt△OCB中,易知 ,r=14.5
,r=14.5
同理,当水面上升3米至EF,在Rt△OGF中可计算出GF= 米,即水面宽度EF= 米.
如图,已知△ABC内接于⊙O, AE平分∠BAC,且AD⊥BC于点D,连结OA.
求证:∠OAE=∠EAD.
已知:如图,⊙O为 的外接圆,
的外接圆, 为⊙O的直径,作射线
为⊙O的直径,作射线 ,使得
,使得 平分
平分 ,过点
,过点 作
作 于点
于点 .
.
(1)求证:
 为⊙O的切线;
为⊙O的切线;(2)若
 ,
, ,求⊙O的半径.
,求⊙O的半径.
如图,在平面直角坐标系中,以点M(0,
 )为圆心,作⊙M交x轴于A、B两点,交y轴于C、D两点,连结AM并延长交⊙M于点P,连结PC交x轴于点E,连结DB,∠BDC=30°.
)为圆心,作⊙M交x轴于A、B两点,交y轴于C、D两点,连结AM并延长交⊙M于点P,连结PC交x轴于点E,连结DB,∠BDC=30°.求弦AB的长;
求直线PC的函数解析式;
连结AC,求△ACP的面积.

已知:AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为r.
(1)如图1,当点E在直径AB上时,试证明:OE·OP=r2
(2)当点E在AB(或BA)的延长线上时,以如图2点E的位置为例,请你画出符合题意的图形,标注上字母,(1)中的结论是否成立?请说明理由.
试题篮
()