已知:如图,在 △ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
求证:BC=CD;
求证:∠ADE=∠ABD;
设AD=2,AE=1,求⊙O直径的长.
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB。
求证: AD⊥DC
如果AD和AC的长是一元二
 次方程
次方程 的两根,求AD、AC、AB的长和∠DAB的度数
的两根,求AD、AC、AB的长和∠DAB的度数
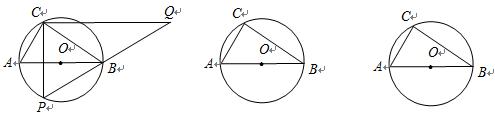
半径为5的⊙O中,直径AB的不同侧有定点C和动点P. 已知BC∶CA=4∶3,点P在弧AB上运动,过点C作CP的垂线,与PB的延长线交于点Q. 求证:△ABC∽△PQC;
当点P与点C关于AB对称时,求CQ的长;
当点P运动到什么位置时,CQ取到最大值?求此时CQ的长;
当点P运动到弧AB的中点时,求CQ的长.
如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
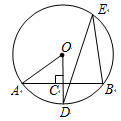
若∠AOD =52º,求∠DEB的度数;
若OC=3,OA=5,求AB的长.
如图,已知 是⊙
是⊙ 的直径,⊙
的直径,⊙ 过
过 的中点
的中点 ,且
,且 ⊥
⊥ ,垂足为点
,垂足为点 .
.
求证:
 是⊙
是⊙ 的切线;
的切线;若∠
 =
= °,
°, =10cm,求⊙
=10cm,求⊙ 的半径.
的半径.
抛物线
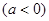 交
交 轴于
轴于 、
、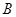 两点,交
两点,交 轴于点
轴于点 ,顶点为
,顶点为 .
.
(1)写出抛物线的对称轴及
 、
、 两点的坐标(用含
两点的坐标(用含 的代数式表示)
的代数式表示)(2)连接
 并以
并以 为直径作⊙
为直径作⊙ ,当
,当 时,请判断⊙
时,请判断⊙ 是否经过点
是否经过点 ,并说明理由;
,并说明理由;(3)在(2)题的条件下,点
 是抛物线上任意一点,过
是抛物线上任意一点,过 作直线垂直于对称轴,垂足为
作直线垂直于对称轴,垂足为 . 那么是否存在这样的点
. 那么是否存在这样的点 ,使△
,使△ 与以
与以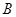 、
、 、
、 为顶点的三角形相似?若存在,请求出点
为顶点的三角形相似?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
(1)求证:点E是边BC的中点;
(2)若EC=3,BD=
 ,求⊙O的直径AC的长度;
,求⊙O的直径AC的长度;(3)若以点O,D,E,C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.
如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,C是圆上一点,连接AC,BC,OA,OB,∠AOE=60°,且OD=4.
求∠ACB的度数.
求AB的长.
一条排水管的截面如右图所示,截面中有水部分弓形的弦AB为 cm, 弓形的高为6cm.
cm, 弓形的高为6cm.求截面⊙O的半径.
求截面中的劣弧AB的长.

如图,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB , CD
, CD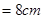

求作此残片所在的圆(不写作法,保留作图痕迹)
求(1)中所作圆的半径
如图①,直线AB的解析式为 (
( )与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A
)与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A
求C点的坐标;
如图②,过
 作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由;
作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由;
在⑵的条件下,连接
 与⊙
与⊙ 交于点G,点P为劣弧G F上一个动点,连接GP与EF的延长线交于H点,连接EP与OG交于I点,当P在劣弧G F运动时(不与G、F两点重合),
交于点G,点P为劣弧G F上一个动点,连接GP与EF的延长线交于H点,连接EP与OG交于I点,当P在劣弧G F运动时(不与G、F两点重合), 的值是否发生变化,若不变,求其值,若发生变化,求出其值的变化范围.
的值是否发生变化,若不变,求其值,若发生变化,求出其值的变化范围.
试题篮
()