初中数学圆幂定理解答题

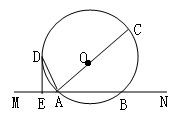
如图，直线MN交⊙O于A、B两点，AC是直径，AD平分∠CAM，AD交⊙O于点D，过点D作DE⊥MN于E.
求证：DE是⊙O的切线
若DE=6cm，AE=3cm，求⊙O的半径．

已知：如图，AB是⊙O的直径，BC是和⊙O相切于点B的切线，⊙O的弦AD平行于OC．求证：DC是⊙O的切线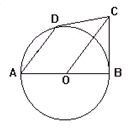

已知AB为⊙O的直径，PA、PC是⊙O的切线，A、C为切点，∠BAC＝30°．
求∠P的度数；
若AB＝2，求PA的长．

如图，AB为⊙O的直径，直线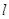与⊙O相切于点C，过点A作AD⊥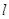于点D，交⊙O于点E．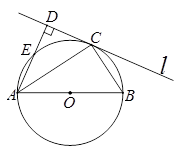

（1）求证：∠CAD＝∠BAC；[（2）若sin∠BAC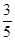＝，BC＝6，求DE的长．

如图所示，点D在⊙O的直径AB的延长线上，点C在⊙O上，且AC=CD，∠ACD=．

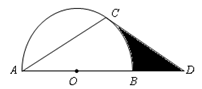
（1）求证：CD是⊙O的切线；
（2）若⊙O的半径为2，求图中阴影部分的面积．

如图，中，，以为直径的交于点，过点的切线交于

求证：
若，求的长．

如图，正方形ABCD中，以BC为直径作半圆，BC=2cm．现有两动点E、F，分别从点B、点A同时出发，点E沿线段BA以1cm/秒的速度向点A运动，点F沿折线A-D-C以2cm/秒的速度向点C运动．当点E到达A点时，E、F同时停止运动，设点E运动时间为t．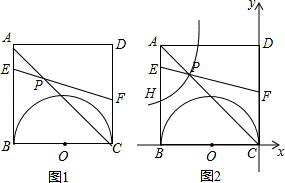

（1）当t为何值时，线段EF与BC平行？
（2）设1＜t＜2，当t为何值时，EF与半圆相切？
（3）如图2，将图形放在直角坐标系中，当1＜t＜2时，设EF与AC相交于点P，双曲线y=（k≠0）经过点P，并且与边AB交于点H，求出双曲线的函数关系式，并直接写出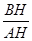的值．

如图，在Rt△ABC中，∠C=90°，∠ABC的平分线BD交AC于点D，DE⊥DB交AB于点E，设⊙O是△BDE的外接圆．

（1）求证：AC是⊙O的切线；
（2）若DE=2，BD=4，求AE的长．

作图：

在同一平面直角坐标系中有5个点：A（1，1），B（﹣3，﹣1），C（﹣3，1），D（﹣2，﹣2），E（0，﹣3）．
（1）画出△ABC的外接圆⊙P，并指出点D与⊙P的位置关系；
（2）若直线l经过点D（﹣2，﹣2），E（0，﹣3），判断直线l与⊙P的位置关系．

已知在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D（如图）

（1）求证：AC=BD
（2）若大圆的半径R=10，小圆半径r=8，且圆心O到直线AB的距离为6，求AC的长．

已知：如图，AB是⊙O的直径，点C．D为圆上两点，且，CF⊥AB于点F，CE⊥AD的延长线于点E．

（1）试说明：DE＝BF；
（2）若∠DAB＝60°，AB＝8，求△ACD的面积．

如图，半圆O直径DE=12，Rt△ABC中，BC=12，∠ACB=90°，∠ABC=30°．半圆O从左到右运动，在运动过程中，点D，E始终在直线BC上，半圆O在△ABC的左侧．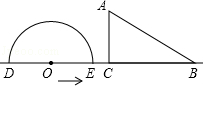

（1）当△ABC的一边与半圆O相切时，请画出符合题意得图形。
（2）当△ABC的一边与半圆O相切时，如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分，求重叠部分的面积

如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）．

（1）将△ABC绕点B顺时针旋转90°得到△A′BC′，请画出△A′BC′；
（2）求BA边旋转到B A′位置时所扫过图形的面积．

如图，已知⊙O的弦CD垂直于直径AB，点E在CD上，且EC=EB．

（1）求证：△CEB∽△CBD；
（2）若CE=3，CB=5，求DE的长．

已知直线AB与轴、轴分别交于点A和点B，AB=10，且tan∠BAO=，以OA、OB为边作矩形OACB，点F 在BC上，过点F作AB的垂线，交AB于点D，交OA于点E，若⊙P是△AOB的内切圆，切点分别为M、N、G，

（1）求证：四边形PMON是正方形；
（2）求⊙P的半径;
（3）求当FE与⊙P相交的弦长为2．4时点F的坐标．