如图,在直角坐标系中,已知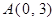 、
、 、
、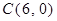 、
、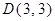 ,点P从C点出发,沿着折线C﹣D﹣A运动到达点A时停止,过C点作直线GC⊥PC,且与过O、P、C三点的⊙M交于点G,连接OP、PG、OD.
,点P从C点出发,沿着折线C﹣D﹣A运动到达点A时停止,过C点作直线GC⊥PC,且与过O、P、C三点的⊙M交于点G,连接OP、PG、OD.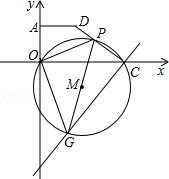
(1)直接写出∠DCO的度数;
(2)当点P在线段CD上运动时,求△OPG的最小面积;
(3)设圆心M的纵坐标为n,试探索:在点P运动的整个过程中,n的取值范围.
如图,在直角坐标系中,⊙P的圆心P在x轴上,⊙P与x轴交于点E、F,与y轴交于点C、D,且EO=1,CD=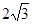 ,又B、A两点的坐标分别为(0,m)、(5,0)
,又B、A两点的坐标分别为(0,m)、(5,0)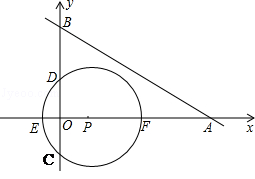
(1)当m=3时,求经过A、B两点的直线解析式;
(2)当B点在y轴上运动时,若直线AB与⊙P保持相交,求m的取值范围.
某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,有如下探讨:
甲同学:我发现这种多边形不一定是正多边形.如圆内接矩形不一定是正方形.
乙同学:我知道边数为3时,它是正三角形;我想,边数为5时,它可能也是正五边形…
丙同学:我发现边数为6时,它也不一定是正六边形.如图2,△ABC是正三角形,弧AD、弧BE、弧CF均相等,这样构造的六边形ADBECF不是正六边形.
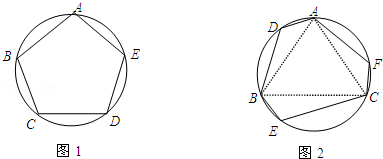
(1)如图1,若圆内接五边形ABCDE的各内角均相等,则∠ABC= °,并简要说明圆内接五边形ABCDE为正五边形的理由;
(2)如图2,请证明丙同学构造的六边形各内角相等;
(3)根据以上探索过程,就问题“各内角都相等的圆内接多边形是否为正多边形”的结论与“边数n(n≥3,n为整数)”的关系,提出你的猜想(不需证明).
已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).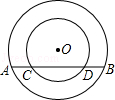
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.
如图,AB为⊙O的弦,C为劣弧AB的中点.
(1)若⊙O的半径为5,AB=8,求tan∠BAC;
(2)若∠DAC=∠BAC,且点D在⊙O的外部,判断AD与⊙O的位置关系,并说明理由.
如图所示,已知圆锥底面半径r=10cm,母线长为40cm.
(1)求它的侧面展开图的圆心角;
(2)若一甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,求它所走的最短路线。
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.
求证:
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)若 ,求⊙O的半径。
,求⊙O的半径。
如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果CD=15,BE=10,sinA= ,求⊙O的半径.
,求⊙O的半径.
已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(1)以AB边上一点O为圆心,过A,D两点作⊙O(不写作法,保留作图痕迹),再判断直线BC与⊙O的位置关系,并说明理由;
(2)若(1)中的⊙O与AB边的另一个交点为E,AB=6,BD= ,求⊙O的半径.
,求⊙O的半径.
如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC= ,DE=3.
,DE=3.
求:
(1)⊙O的半径;
(2)弦AC的长;
(3)阴影部分的面积.
已知,如图,四边形ABCD内接于圆,延长AD、BC相交于点E,点F是BD的延长线上的点,且DE平分∠CDF.
(1)求证:AB=AC;
(2)若AC=3cm,AD=2cm,求DE的长.
试题篮
()